Modelling linguistic accommodation |
|

0
For example, you may come across definitions like this: “A finite state automaton is a quintuple (\(Q\), \(\Sigma\) , \(q_0\), \(F\), \(\delta\)) where Q is a finite set of states (\(q_0\), \(q_1\), …, \(q_n\) ), \(\Sigma\) is a finite alphabet of input symbols, \(q_0\) is the start state, \(F\) is the set of final states \(F \in Q\), and \(\delta \in Q \times \Sigma \times Q\), the transition function.”
That definition should be taken outside and shot. 3
‘Accommodation’ is that thing where you automatically mimic the person you’re talking to. You might immediately think of baby talk and speaking loudly to old people, but these conscious games are not what I’m talking about. For humans also unconsciously shift speech, depending on the gender, status, and likeability of their interlocutor. Accommodation is pervasive, correlated with key bits of human interaction: empathy, status, and teamwork. Studying accommodation puts you at the intersection of statistical modelling, linguistics and social signal processing.
The trick is to detect it using Hidden Markov models (HMMs). A technique from speaker verification is adapted: model-conditional probabilities estimate the ‘distance’ of each speaker, from their interlocutor, for each word. This likelihood ratio is taken for each word uttered by a speaker, relative to their interlocutor uttering it. The correlation of these ratios over time is used to infer the presence of accommodation and estimate effect sizes.
I used the dataset from Stuart-Smith et al (2015) (henceforth “SSSV” after the surnames of the authors): n=120,000 words, from 6 pairs of speakers. The modelling and data analysis was implemented in Python, with modelling tools from the ‘Hidden Markov Toolkit’ (HTK). 2
1. Introduction
To help locate us, let’s define some subfields of computational linguistics:
- Speech processing: The analysis of speech as a digital signal (and thereby as a mathematical object). As opposed to
- Natural language processing (NLP): The analysis of speech as symbolic information, as syntax and semantics (and thereby as a mathematical object).
- Paralinguistics: The analysis of the ‘supra-segmental’ parts of communication: including rhythm, pitch, volume and intonation. (That is, of those components that extend over multiple units of speech, e.g. phonemes.)
- Social signal processing (SSP): The analysis of interaction context (i.e. of properties beyond the literal communication). Involves automated inference from data to phenomena that cannot be directly observed, but only inferred from correlated behaviours.
We use techniques from each of the above: from speech processing, the vectorization of speech waves for tractable model inputs; from NLP, we adapt a mechanism (the general ‘recogniser’) initially developed for automatic word recognition; we incorporate paralinguistic content in considering more than the symbolic or phonemic content of speech; and in line with SSP we are attempting to make inferences about a social process indirectly.
The goal is an objective, holistic, and automatic approach to linguistic accommodation. The speakers are represented using Hidden Markov models (HMMs), long the dominant tool for acoustic modelling. 5
To very briefly introduce the analytical method: We begin with no models of the speakers, no model parameters, and no known general laws of accommodation to apply. What we do have are twelve sets of time-annotated speech signals (one set per speaker, with each signal representing a task completed by that speaker) and a fully general signal-modelling framework (i.e. HMMs).
The tractability and performance of HMMs depends on three powerful dynamic programming algorithms: Baum-Welch re-estimation (for learning model parameters from training data); Viterbi decoding (for inferring an optimal processing for each given observation sequence); and Forward-backward smoothing (for inferring the probability of an observation sequence given a state sequence and a model).
Our unit of analysis is the ‘speaker-task’ (that is, one of the conversational prompts completed by each of 12 speakers of the dataset). The sub-units are the words spoken by each speaker during this task, with frames within each word serving as important sub-sub-units (see Section 5.2 for a schematic view of the data).
Each speaker is modelled as an HMM; these models are used to estimate the likelihood ratio (a measure of the relative extent to which each model explains or predicts each word) for each word in the test set. For each task completed by each speaker, these ratios are combined into correlations of the pair’s ‘distance’ over the time of an eight-minute conversation. The sign and significance of the time correlation between these ratios is used to infer the presence of accommodation, and to estimate effect sizes. (See Fig.9 for a schematic view of this calculation.)
The use of likelihood-ratio correlations to measure the relative distance between speakers was first developed for authenticating speaker identity.
Overview of this dissertation:
The pipeline is given in Table 1. In the following, Stages (a) through (c) are referred to as ‘the SSSV experiment’. The rest of the introduction gives definitions and methodology for accommodation research. Section 2 defines the formalism used.
Section 3 lays out the abstract theory of modelling sequences with finite-state machines, and then of Markov and Hidden Markov models.
Section 4 applies the HMM framework to the study of speech, particularly speaker verification and accommodation.
Section 5 explains the experimental setup and the implementation of our HMMs; section 6 lays out key results from evaluating them.
Section 7 concludes with discussion, limitations, and potential connections to future work.
| Stage | Operation | Conversion | |
|---|---|---|---|
| Experiment | a) Logistics | Design, recruitment, conversation elicitation | From tasks to air-pressure waves (conversations). |
| b) Data collection | Recording task-oriented conversations via ‘Diapix’ prompts. | From conversations to wave recordings. | |
| Preparation | c) Annotation | Manual tagging by word, phoneme, and precise timing. Then "segmentation" of each conversation into words. | From one conversation waveform to 109,730 waveforms tagged by time and word. |
| d) Feature extraction | Parameterisation of speech recordings. Also labelling vector sequences. | From waveforms to vector representations. | |
| Modelling | e) Train | Global means and variances. Decoding and Baum-Welch re-estimation | From generic HMMs + training data, to trained models. |
| f) Test | The Forward-Backward algorithm (EM) for each word. | From trained models and test data, to conditional probability transcriptions for model pairs. | |
| Analysis | g) Likelihoods | Subtraction of {log-likelihood given own model} from {log-likelihood given pair’s model} | From conditional probability transcriptions to likelihood ratios (point speaker-distance estimates). |
| h) Correlations | Spearman’s rank correlation between time and likelihood ratios. | From speaker-distances to correlations over time. | |
| i) Inference | Thinking. | From correlations to this essay. | |
Table 1. The project
1.1. What is linguistic accommodation?
Accommodation is
the tendency of people involved in an interaction to converge towards [or diverge from] common behavioural patterns. 8
Thus, linguistic accommodation is where speakers come to talk more (or less) similarly as they interact. It is fundamental to human communication, closely correlated with key aspects of interactions including empathy, status, co-ordination, and team effectiveness (especially in task-oriented interactions). 9 10
A note on navigation: Depending on the particular behaviour being emphasised, accommodation is sometimes known as ‘interpersonal adaptation’, ‘synchrony’, ‘convergence’, ‘(nonconscious) mimicry’ or ‘mimesis’, ‘alignment’, ‘spontaneous imitation’, and sometimes ‘entrainment’ (after the phenomenon of coupled oscillators in physics).
Accommodation has been experimentally detected in many aspects of speech including: speakers’ fundamental frequency 11; phonemes 12 13 ; speech rate 14 and rhythm 15 ; as well as higher-level aspects of language like accent 16 and vocabulary. 17 While pervasive, accommodation may not be too dramatic in effect size. The holistic analysis of the SSSV experiment found \(R^2 = 0.11 \pm 0.04\); my analysis found effect sizes half this strong. 18
It is usually treated as the unconscious tendency to converge, independent of intentional flattery; certainly the effect has been seen to occur in cases without conscious intention to mimic (for instance in the experiments of Chartrand and Bargh (1999), in which experimenters’ mannerisms were accommodated by participants without their being aware of doing so). 19
The effect has been seen to vary by the degree of mutual liking between interlocutors 20 , differences in social status21, and by gender matching (that is, people accommodate more to interlocutors of their own gender).22
Various evolutionary rationales have been presented to explain the pervasiveness and apparent power of the phenomenon in human life: in terms of the recency effect in episodic memory (by which one’s language depends strongly on the language most recently heard), of displaying one’s group affiliation, or of approval-seeking.23
Some variant of them is bound to be true; but these go
well beyond the scope of the present work, which is focussed on existence and effect size, rather
than causal direction or ancestral origins.
1.2. Measuring accommodation
We can divide studies of accommodation by methodology:
- whether the measurements made are objective, or subjective (and quantitative or qualitative);
- whether the acoustic evaluation is holistic, or reductive (that is, whether the signal is taken as one variable, or analysed only in terms of particular spectral or syntactic components);
- the temporal scope of the analysis (whether the phenomenon is studied at the conversation level or by short ‘reduced stimuli’);
- whether the interactions analysed are guided by experimenters, or are free-form.
The present work aims for an objective, holistic measure of accommodation, with data analysed at the conversation level, and the conversations guided by task prompts. Precedents for this specific approach are relatively scarce in the literature, but Lelong and Bailly (2011) provide a good example of the approach, in speech recognition. 24
We attempt to use all the acoustic evidence – to capture the signal interactions within a conversation that may produce accommodation – whilst retaining the analytical power to detect the relatively subtle phenomenon. (Holistic processing also has the advantage of reflecting the manner in which humans perceive speech signals: as a whole, rather than a logical composite of parts.)
Most accommodation research does not take the conversation as the unit of analysis, even though accommodative effects are consistently found across supra-segmental features of speech (where ‘supra-segmental’ denotes effects that are longer-term than any given unit, e.g. phoneme, word or sentence).
The general approach is to measure effects using ‘reduced stimuli’, marginal units: the reasoning being that, if accommodation can be detected to occur given only minimal acoustic cues, then the findings can be called robust. (The popularity of this method can be seen in the papers listed in this footnote 25, comprising a substantial fraction of all accommodation experiments found.)
Setting the scope of analysis at the conversation level should allow accommodation to manifest, and fills a gap left by the proliferation of careful segmental reductionist research.
2. Glossaries
Linguistics Glossary
- Utterance: a token of a speaker: here, one word decomposed into a sequence of vectors, i.e \(O^{(A)}_i\). (Used in place of ‘word’, since the latter is ambiguous between the symbol – the type – and the individual waveform – the token.)
- Speech processing: The analysis of speech as a digital signal (and thereby as a mathematical object). As opposed to
- Natural language processing (NLP): The analysis of speech as symbolic information, as syntax and semantics (and thereby as a mathematical object).
- (Automatic) speech recognition (ASR): NLP for words. The decoding of speech signals into the most likely words (or sentences).
- Paralinguistics: The analysis of the ‘supra-segmental’ parts of communication: including rhythm, pitch, volume and intonation. (That is, of those components that extend over multiple units of speech, e.g. phonemes.)
- Social signal processing (SSP): The analysis of interaction context (i.e. of properties beyond the literal communication). Involves automated inference from data to phenomena that cannot be directly observed, but only inferred from correlated behaviours.
- Speaker verification: Particular task in speech processing: given a speaker model, how likely is it that some new speech sample is by that speaker? The decoding of speech signals to the most likely speaker.
- Speaker distance: the likelihood ratio of the model of the actual speaker (\(A\)) of an utterance \(o_t\) generating \(o_t\), relative to the likelihood of their interlocutor model (\(B\)) generating \(o_t\).
- Finite state-machine (FSM): An abstract computer used to generate or test sequences of symbols. It consists in 1) a set of states, 2) a set of links (“transitions”) between these states, and 3) an alphabet of symbols labelling these links. An FSM transitions from its current state, to one of its connected states once per time step, and emits an observation every time a state is entered.
- Probabilistic finite-state machine (PFSM): A tool for representing probability distributions over sequences of observations. A family of nondeterministic models that change state and emit signals according to the current emission function (the density function of the current state).
- Transition probability: \( p( S_t | S_{t-1} ) \); the chance of the PFSM switching from state \( S_t \) to \( S_{t-1} \)
- Emission probability: \( p( o_t | S_{t} ) \); the chance of observing \( o_t \)on entering state \( S_{t} \).
- Markov model: A stochastic model, representable as a PFSM, in which the Markov property holds (that is, in which the transitions between each state depend only on the most recent antecedent state).
- Hidden Markov model: A Markov model in which the data-generating process is hidden, but observations dependent on the states are available. Thus, an HMM is a joint probability distribution over outputs and hidden states, \( p(O|S) \).
The number of states in the model is the number of 'sections' the input sequence is treated as having. State transitions are determined by a transition matrix (i.e. a prior probability distribution); on entering a state, a vector is generated from the new emission function (the distribution associated with the state being entered). This is illustrated in Fig.3. - Learning: Determining optimal model parameters from training data (see section 3.1.2).
- Decoding: Determining an optimal sequence of states, given an observation sequence.
- Evaluation: Determining the total likelihood of an observation sequence, given a trained model and a decoding.
- Gaussian mixture model: A weighted sum of \(G\) unimodal Gaussian distributions.
- Ergodicity. Whether model states can transition to all other states.
- Directionality. Whether model states can transition backwards as well as forwards.
- Self-looping. Whether states can ‘transition’ to themselves.
- Skips. Whether state transitions can bypass the next indexed state.
- Forward-backward algorithm: Dynamic programming algorithm used both in training the HMMs (to find an input to the Baum-Welch procedure – the probability of being in a given state at a given time) and in the ‘total likelihood’ evaluation of each utterance.
- Frame: A fixed-length portion of a speech signal, from which to extract a feature.
- Windowing: The subdivision of a signal into successive frames. (Perhaps overlapping frames, as here.) The resulting windows are multiplied by a ‘window function’ that eliminates the signal lying outwith the present interval.
- Extraction rate: how often the processor takes a window from the signal. Here, 10ms.
- Window size: the length of each window. Here, it is 25ms long. So we have overlapping windows.
- Mel-Frequency Cepstral Coefficients (MFCCs): Type of acoustic vector. Uses cepstral coefficients from a Fourier transform of the original waveform.
- Linear predictive coding (LPC): early digital speech encoding scheme. Rather than storing all information from a signal, we can model signals by estimating the magnitude of the signal at \(t\) as a linear combination of the previous \(p\) samples. The resulting feature vector is just a sequence of linear coefficients plus a set of errors.
Mathematical Glossary
Indices
| \( A \) : | a speaker. |
| \( B \) : | another speaker, interlocutor with A. |
| \( \theta_A \) : | a model of A (that is, a HMM trained on vectors from words by A). |
| \( \theta_B \) : | model of B, A's interlocutor. |
| \( i \) : | index of given word |
| \( j \) : | index of given coefficient |
| \( k \) : | index of current task |
| \( t \) : | index of given time |
| \( T \) : | total number of frames |
| \( Ta \) : | task; a conversation |
| \( n_i \) : | no. of frames extracted from word i |
| \( N_{(A)}\) : | total no. of words spoken by speaker A |
| \( N^{(A)}_k\) : | total no. of words spoken by A during task k. |
| \( BW \) : | for Baum-Welch. Denotes training data. |
| \( V \) : | for Viterbi. Denotes test data. |
| \( g \) : | index of current Gaussian |
Hyperparameters
| \( D \) : | the dimensionality of the vector space of features. (Here, 12.) |
| \( G \) : | no. of Gaussians in each mixture model. (Here, 10.) |
Data structure
| \( o_t \) : | an observation at time \(t\); a 12D vector representing one frame of one word waveform. (Also depicted as \( o^{(A,i)}_j\), see below.) |
| \( O^{(A)}_i = ( o^{(A,i)}_1, o^{(A,i)}_2, ... o^{(A,i)}_n) \) : | an utterance (or, the sequence of observations extracted from word \(i\) spoken by \(A\) ) |
| \( O^{(A)} = \{ O^{(A)}_i \} \) : | all words spoken by \(A\) (or, the set of sequences of observations taken from words spoken by \(A\) ). Also equivalent to \( Ta^{(A)} \), all the tasks of \(A\). |
| \( o^{(A,i)}_j = o_t \) : | a frame (vector \( \large[ o^{(A,i,j)}_1, o^{(A,i,j)}_2, ..., o^{(A,i,j)}_D \large] \) of coefficients taken from word spoken by \(A\) |
| \( Ta^{(A)}_k \) : | all words spoken by \(A\) during task \(k\) (the set of sequences of observations extracted) |
Modelling
| \( \theta_A \) : | the HMM parameter set. Exhausted by \( \{ N_S,M, Tr^{(A)}, E^{(A)} \} \) : |
|
|
| \( E_j \) : | the GMM emission function for state \(j\). Exhausted by \( \{ \pi, \sigma, \mu \} \): |
|
|
| \( S^{(A)}_i \) : | a state sequence taken by \( \theta_A \) while processing a word \( i \) |
| \( S^*_i \) : | an optimal state sequence given word \( i \). |
| \( s(t) \) : | the state of the model at time \(t\) |
| \( \alpha_j(t) \) : | the Forward probability (sum of being in state \(j\) at time \(t\) ). |
| \( \beta_j(t) \) : | the Backward probability of being in state \(j\) at time \(t\). |
| \( L_j(t) \) : | the probability of the HMM occupying state \(j\) at time \(t\). |
Inference
| \( d^{(A)}_i = \frac{ p(O_i^{(A)} | \theta_A }{ p(O_i^{(A)} | \theta_B } \) | speaker-distance: the likelihood ratio of \(A\) making an utterance, relative to \(B\) doing so. |
| \( t_i^{(A)} \) : | the time at which speaker \(A\) uttered word \(i\). |
| \( \rho \large(\,\, t_i^{(A)}, d^{(A)}_i \large) \) | Spearman’s rank correlation between paired time & speaker-distance. |
3. Sequence modelling with state machines.
Abstractly, we can consider any speech signal as a statistical sequence of observations . For a multi-level phenomenon like speech, the terms of \(O\) might be words, phonemes, or lower-level features like vectors of spectral coefficients extracted from the signal. The signal is treated statistically in order to make the analysis tractable, to handle the massive variability found between tokens of linguistic symbols, and because of the automation it offers: the models we need can be optimised given just data and some initial guesses. 27
This consideration made, we can define the pattern recognition (or sequence analysis) problem as: “How do we get a probability density function for the space of these sequences?”
There are two rough approaches:
Generative models, which first describe the underlying data-generating process for \(O\) as a model \(\theta\), then categorises tokens of that process by computing the probability of \(O\) conditional on the model, i.e. \(p(O | \theta)\)
Or discriminative models, which don’t model the original process, but instead directly categorise tokens via taking a conditional probability distribution over the signal, i.e. \(p( \theta \,|\, O )\). 28
In linguistics, we generally want to map \(O\) to a series of symbols, ‘decoding’ the signal into one or other familiar categories, as in:
- (Automatic) speech recognition (ASR): The decoding of speech signals into the most likely words (or sentences).
- Speaker verification: The decoding of speech signals to the most likely speaker.
“The most important computational technique in spoken language processing” is a type of generative model called the finite-state machine. 29
- Finite state-machine (FSM): An abstract computer used to generate or test sequences of symbols. It consists in 1) a set of states, 2) a set of links (“transitions”) between these states, and 3) an alphabet of symbols labelling these links.
An FSM transitions from its current state, to one of its connected states once per time step, and emits an observation every time a state is entered.
Given a topology defining the structure of acceptable sequences, FSMs can be used to generate valid sequences of symbols incrementally or, equivalently, to check input sequences for validity.

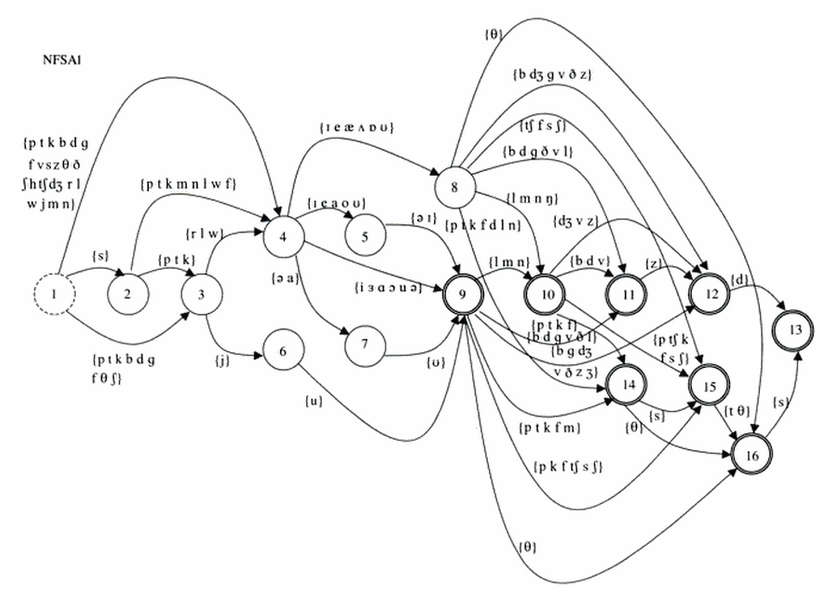
Fig.1 - A finite state machine for checking if phoneme strings are English-like.
(Circles are states, lines are transitions.)
Since our object of study is neither a deterministic grammar nor a simple non-deterministic set of
acceptable strings, we need the sub-family of FSMs that can handle stochastic distributions of observations:
- Probabilistic finite-state machine (PFSM): A tool for representing probability distributions over sequences of observations. A family of nondeterministic models that change state and emit signals according to the current emission function (the density function of the current state).
- Transition probability: \( p( S_t | S_{t-1} ) \); the chance of the PFSM switching from state \( S_t \) to \( S_{t-1} \)
- Emission probability: \( p( o_t | S_{t} ) \); the chance of observing \( o_t \)on entering state \( S_{t} \).
Each state has an emission function \(p(o_t | \theta)\), where \(\theta\) is a model / parameter set learned from training data (observations labelled by correct symbols); the model overall has a transition matrix which determines the probabilities of moving from each state to each state.
(This can include remaining in the same state, or “self-looping”.)
3.1. Markov and Hidden Markov models
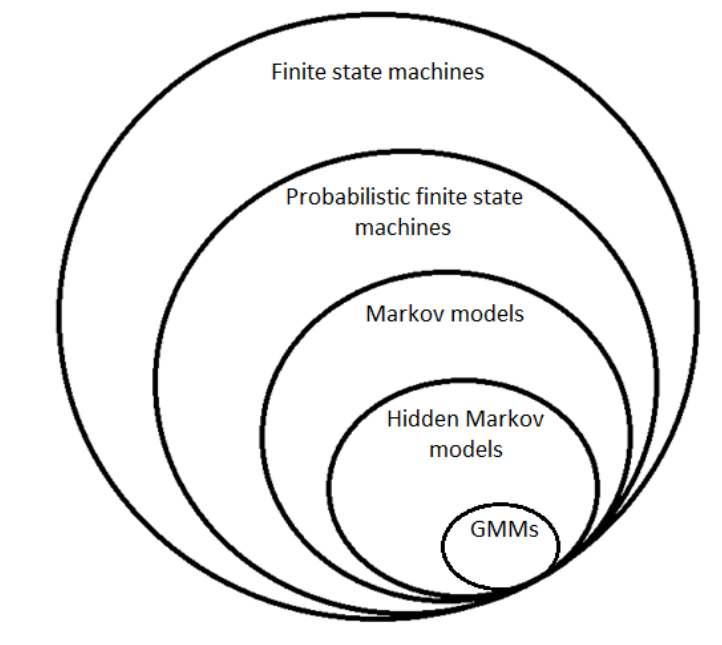
Fig.2. The relation between key classes of automata, as nested sets.
In speech, as with many real-world signals, the observation sequence is of too high dimensionality to directly estimate its joint conditional probability \(p(o_1, o_2, ...o_n | \theta)\) from examples of words (or, for us, from examples of words betokening a speaker).
To reduce the problem from estimating the class-conditional densities over arbitrary dimensions, we assume that the speaker is a parametric model (that is, has a fixed number of parameters).
This limits a priori the distributions our model can use, but estimating these parameters is a much simpler and tractable problem.
The most common parametric model in linguistics is the Markov model:
- Markov model: A stochastic model, representable as a PFSM, in which the Markov property holds (that is, in which the transitions between each state depend only on the most recent antecedent state).
$$ p(S_1, ... S_n) = \prod_{i=1}^n \,\, p(S_i | S_{i-1}) \qquad\qquad (E1)$$
In cases where the signal-generating process (the state sequence) is not itself observable, but must
be inferred from the emitted observations, call the Markov model a hidden Markov model. These
models are doubly stochastic: the underlying stochastic process (the state sequence) is inferred via
another set of stochastic processes (the observation sequence).
- Hidden Markov model: A Markov model in which the data-generating process is hidden, but observations dependent on the states are available. Thus, an HMM is a joint probability distribution over outputs and hidden states, \( p(O|S) \).
The number of states in the model is the number of 'sections' the input sequence is treated as having. State transitions are determined by a transition matrix (i.e. a prior probability distribution); on entering a state, a vector is generated from the new emission function (the distribution associated with the state being entered). This is illustrated in Fig.3.
An HMM is built and used in three stages:
- Learning: Determining optimal parameters from training data (see section 3.1.2).
- Decoding: Determining an optimal sequence of states, given an observation sequence.
- Evaluation: Determining the total likelihood of an observation sequence, given a trained model and a decoding.
Though based on Andrey Markov’s century-old theory, the HMM itself was first formalised in the 60s31 and the applied method has flourished only in the last twenty years.32
Some resulting statistical properties of HMMs
- Statistical recovery of an unknown or underspecified process. i.e. The approach can be applied even where a target process is not repeatable, or a target data sequence (\(S\)) cannot itself be directly observed, as long as we are given an observable sequence (\(O\)) conditional on the target.
- Statistical independence. The structure of HMMs allows us to assume: 1) that state transitions are conditionally independent of all prior and posterior states, except for the state immediately prior; and 2) that each observation is conditionally independent of all other observations.
- Efficient parameter learning. We can efficiently obtain good estimates for the transition and emission function parameters by recursive expectation-maximisation over a training set (see section 3.1.2 below).
- Implicit modelling. Given at least locally optimal parameters, HMMs implicitly model the
typical instance of a linguistic unit, as well as the ranges of variability to expect between
different tokens of the same unit. (Here, our unit is the typical word-independent utterance
of one speaker).
This is fundamental to the present methodology, in which a holistic analysis of the acoustic evidence is sought, and where no sufficient analytical understanding of the process exists (e.g. a law-like neuroscientific model of accommodation). - Representation of more complex observation patterns. The HMM’s stochastic emission functions allow for differing patterns of observations conditional on the state. This includes modelling continuous parameters via multivariate continuous-density distributions like the Gaussian Mixture model. GMMs have further properties, e.g. multiple modes and non- symmetrical input vectors (see Section 3.1.1).
3.1.1. Representing HMMs
The HMM is a complex concept. So it’s useful to illustrate all the different ways we’re using it:
Represented in algebra as a parameter set \(\theta\):
$$ \theta_A = \{ N_S,M, \pi^{(A)}, Tr^{(A)}, E^{(A)} \} \qquad\qquad\text{(E2)} $$ (Which is to say: a hidden Markov model is specified completely by the number of emitting states in the model \(N_S\); the symbols emitted per transition \(M\); a set of initial state probabilities \(\pi^{(A)}\); a transition function \(Tr^{(A)}\); and \(E^{(A)}\) a set of emission functions.)
Or as state diagram:
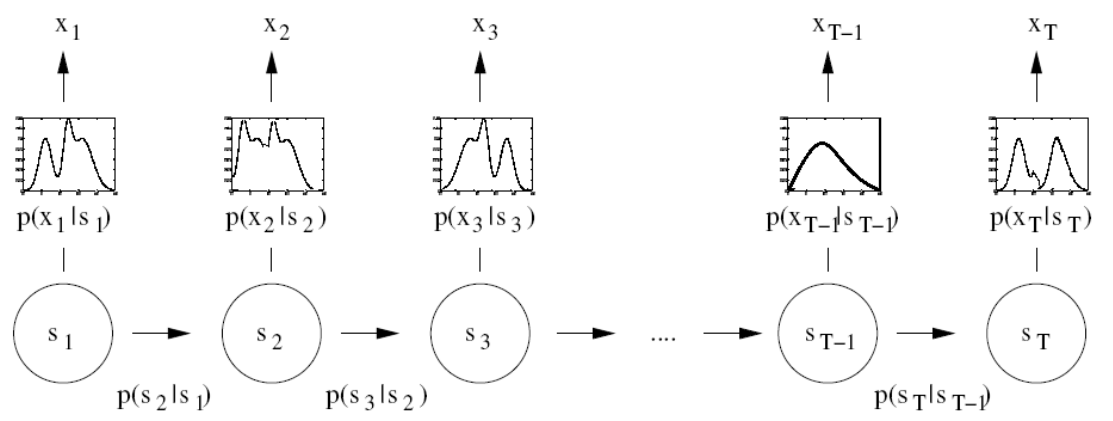
Fig.3 - A simple no-skip Left-Right HMM, showing each state \(S_1, ...S_T\)
with a transition probability \( p(S_j | S_j-1)\), and an emission probability distribution
yielding observation \(x_j \) with \( p(x_j | s_j) \).
Figure 3 illustrates the differing emission function of each state: a state is thus a joint probability distribution over a prior distribution (for controlling transitions) and a conditional distribution (for controlling the emission of observation vectors).Or as the joint probability of observation sequence \(O\) given state sequence \(S\):
$$ P(S,O^{(A)} | \theta_A ) = P(O^{(A)} | S,\theta_A) \times P(S | \theta_A) \qquad\qquad\text{(E3)} $$
This inverse-probability calculation represent what an HMM ends up inferring. But for us the state sequence \(S\) is unknown for each input observation sequence. So, read at face value, (E3) denotes a visible Markov model, not an HMM; we must instead compute the ‘total likelihood’ of our current observation sequence, by summing over all possible state sequences of length \(T\).Or as the total likelihood of \(O\) for an unknown state sequence \(S\):
That is, we take the product of the probability of entering an initial state, multiplied by the product of all transition probabilities, multiplied by the product of all emission probabilities for each successive component of the observation sequence \(O\):
$$ P(O^{(A)} | \theta_A ) = P(S_1 | S_0) \times \prod_{T=2}^T \,\, P(S_t | S_{t-1}) \times \prod_{T=1}^T \,\, P(o_t | S_{t}) \qquad\qquad\text{(E4)} $$Or as computable definition:

Fig.4 - The code for a two-state GMM-HMM representing speaker ‘ARA14’Or, finally, by topology:
Finally, we can categorise HMMs by key parameters:
- \(N\). (Number of states per model.) Single-state HMMs do not take into account the temporal information in the sequence; they can thus be usefully considered a separate class, the 'GMM' (see Section 3.1.1 below).
- \(S\). (Continuous or discrete states.) In the following, only HMMs with discrete state spaces are considered; extensions of the models to continuous hidden variables exist, but were not applied.
- \(M\). (The alphabet size.) In a sense, the alphabet of each of the present HMMs is of size 1; the models only seek to recognise one speaker at a time, and simply report a probability of this being the case. In another sense, we have a meta-alphabet of 12 (i.e. one symbol for each different speaker.)
- \(E\). The nature of the emission function. In each model below, the emission functions are a mixture of ten Gaussians, making the models Gaussian-mixture-model hidden Markov models (GMM-HMMs).
- \(MO x\). The order of the Markov property; i.e. how many prior states the transitions are conditionalised upon. The present models are all first-order Markov models, as defined in equation (E1).
- \(T\). The model topology, as embedded in the transition function:
- Ergodicity. That is, whether all states can transition to all other states. The present models are non-ergodic.
- Directionality. Whether states can transition backwards as well as forwards. The models here developed are ‘Left-Right’ models, allowing only transitions of nondecreasing index, as in (E5): $$ \forall \, ij \,\, | \,\, i \lt j, \quad p(s_i | s_j) = 0. \qquad\qquad \text{(E5)} $$
- Self-looping. Whether states can ‘transition’ to themselves at a time step. All states in the present models allow self-looping; this property is: $$ \forall \, i \,\,\, p(s_i | s_i) \neq 0 \qquad\qquad \text{(E6)} $$
- Skips. Whether state transitions can bypass the next indexed state. The present models disallow this; the no-skip property is defined in (E7): $$ \forall \, ij \,\,\, |\, (s_i \rightarrow s_j)\, \& \,\, i \lt j, \quad (j - i) = 1. \qquad\qquad \text{(E7)} $$
The baseline models used in this paper are Left-Right, self-looping, no-skip, continuous-density,
discrete-state, diagonal-covariance, first-order GMM-HMMs. 33 This topology is assumed throughout.
3.1.2. Gaussian mixture models (GMMs)
To reiterate: the emission function of each state of each HMM is implemented as a Gaussian mixture
model (GMM), a further nested stochastic process for the system:
- Gaussian mixture model: A weighted sum of \(G\) unimodal Gaussian distributions. The parameters for an GMM-HMM’s emission function are simply: $$ E^{(A)} = \{ \pi^{(A)}, \sigma^{(A)}, \mu^{(A)} \} $$ (Where \(\pi^{(A)}\) is a set of \(G\) sets of mixture coefficients (one set per state); \(\sigma^{(A)}\) is a set of \(G\) covariance matrices; and \(\mu^{(A)}\) a set of \(G\) means. Note that in the present model set only diagonal covariances are used. The mixture weights are probabilities, and so must follow ∑ and .)
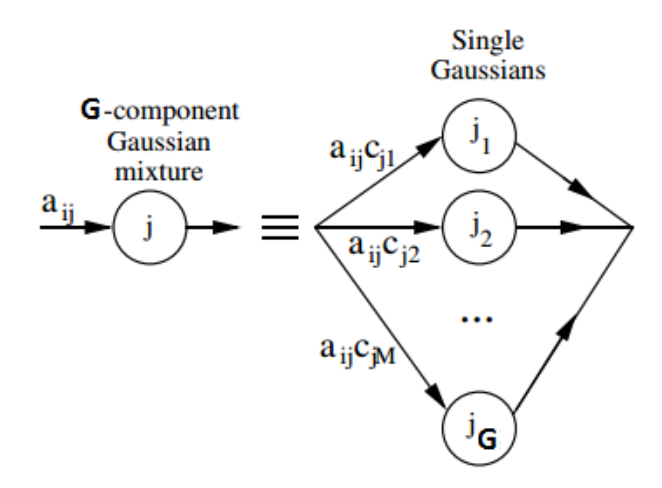
Fig.5. Each individual state of a HMM is itself a set of \(G\) sub-states,
the Gaussian components \(j_g\).
The probability of generating an observation from a GMM is the {sum of the probability of selecting each Gaussian component ( \(\pi_G\) )} multiplied by the {probability of generating \(o_t\) from that Gaussian}:
\[P(O^{(A)}_t \, | \,S_j) = \sum_{g=1}^G \,\, \pi_g \,\times\, \mathcal{N}\, \large( o_t, \mu_{jg}, \sigma_{jg} \large) \qquad\qquad \text{(E8)}\]Where \(\mathcal{N}\) denotes the normal distribution. The product in (E8) can be understood by saying each state of an HMM possesses \(G\) sub-states, the choice of which is a discrete latent variable, illustrated in figures 5 and 6.
HMMs are actually a generalisation of GMMs in which the mixture weights that select the emission function for each observation are dependent on a Markov process (i.e. the multiple states and their conditional transitions), rather than being independent constant probabilities, as in figure 6. That is, a GMM is a single-state HMM.
As such we can generalize (E8) for HMMs: the probability of an HMM generating an observation sequence \(O^{(A)}_t\) is:
\[P(O^{(A)}_t \, | \,\theta_A) = \prod_{j=1}^n \,\, \large(\,\, \sum_{g=1}^G \,\, \pi_g \,\times\, \mathcal{N}\, \large( o_j^{(A,i)}, \mu_{g}, \sigma_{g} \large) \,\,\large) \qquad\qquad \text{(E9)}\]Where \(j\) is the present frame of word \(i\) and \(n\) is the number of frames taken from \(i\). i.e. When evaluating a given sequence of observations, the GMM-HMM takes the product of the probability sums of (E8).
Finally, consider some useful properties of GMMs:
- Flexibility. GMMs are able to model asymmetrical input vectors, as well as multiple modes in the data distribution.
- Multiple modes. The characteristic spectral signature of different speakers can manifest as multiple modes. Some indication of how this happens is given in the discussion of MFCC features in Section 5.2.d).
- Tractable parameter estimation. The GMM’s simple parameters, particularly the use of high-order (but diagonal) covariances, serve to preserve the tractability of the parameter algorithms for HMMs.
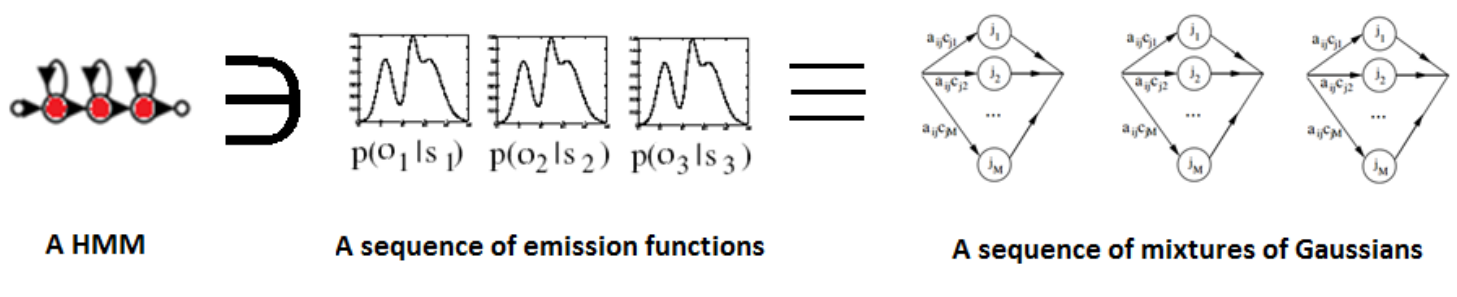
Fig.6 - A HMM considered as a nested state diagram: a series of sets of Gaussians.
3.1.3. Designing HMMs
In his essential introduction to HMMs37, Lawrence Rabiner lays out the three basic problems of
designing HMMs and the standard algorithms used to overcome them:
Conditional evaluation
: given a model \(\theta_A\), what’s the probability of a given observation sequence \( o_t\), or set thereof \( O^{(A)}\)?
: We use the Forward-Backward algorithm to find this: it is the sum of probabilities of generating \(O\), given all different state sequences it arises in (see equation E3, above or): $$ p(O^{(A)} | \theta_A) = \sum_{s \in S} \,\, P(S, O^{(A)} \, | \, \theta_A ) \qquad\qquad \text{(E10)} $$ Or thirdly in terms of the forward probability \(\alpha_i \) at time \(t\): $$ p(O^{(A)} | \theta_A) = \sum_{j = 1}^{N} \,\, \alpha_i(t) \, \times \, P( S_N | S_i ) \qquad\qquad \text{(E11)} $$Best decoding
: how to choose an optimal state sequence \(S*\) through \(\theta_A\)?
: We use the Viterbi algorithm to find the likeliest state sequence, such that: $$ S^* = arg \,max \,\, P(S \,|\, O^{(A)}, \theta_A) \qquad\qquad \text{(E12)} $$
(NB: For our purposes – isolated ‘word’ [speaker] recognition – the Viterbi algorithm is actually unnecessary, since the forward probability calculation provides us with a total likelihood.38)Model learning
: How do we choose model parameters that maximise the likelihood of the training data, \( P(O_{BW} \,|\, \theta_A) \)?
We use Baum-Welch re-estimation to find the optimal parameters given a training set: $$ \theta_A^* = arg \,max \,\, P( O_{BW} \,|\, \theta_A) \qquad\qquad \text{(E13)} $$ This makes use of the Forward-Backward algorithm, to determine the total likelihood of a sequence over all state sequences that could generate it. (We go on to describe this vital machinery.)
3.2. Dynamic programming algorithms for HMMs
3.2.1. Forward-Backward smoothing
The forward-backward algorithm is used in training the HMMs (to find an input to the
Baum-Welch procedure – the probability of being in a given state at a given time) and in the ‘total
likelihood’ evaluation of each word. It involves the calculation of:
a. the forward probability (joint probability of producing \(O\) and ending in state \(j\);
b. the backward probability (conditional probability of completing sequence \(O\) given start state \(j\));
c. and smoothing: the product of (a) and (b): a measure of the distribution of states over \(O\).
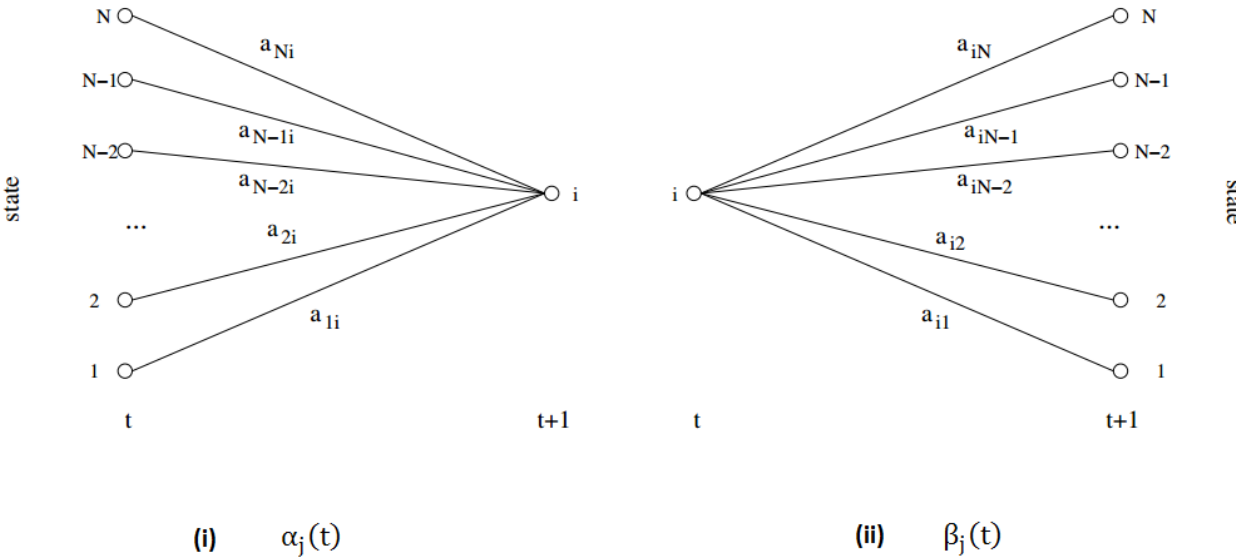
Fig.7 - Calculating forward \(\alpha\) and backward \(\beta\) probabilities.
The following is repeated for each time step:
(i) forward: sum probabilities of all the possible transitions to a given state (i) at time (t);
(ii) backward: then sum probabilities of transitions leading from state (i) for the remainder of the observation sequence.
Calculating the forward probability.
The forward ‘probability’ 40 - \(\alpha_j^{(A)}(t)\) - is the joint probability of observing the first \(t\) vectors of \(O\) and subsequently ending up in state \(j\) at time \(t\), i.e. \( P (\, o_1, ..., o_t \, , \, s(t) = j \,)\): $$ \alpha_j(t) = P (\, [o_1, ..., o_t] \, , \, [s(t) = j] \,|\, \theta_A) \qquad\qquad \text{(E14)} $$
In practice a recursive pruning form is used: $$ \alpha_j(t) = \large[\, \sum_{i=1}^N\, \alpha_i(t-1) \, \times \, P(S_j | S_i ) \,\large] \,\,\times \,\, P(o_t \,|\, S_j ) \qquad\qquad \text{(E15)} $$ where \(N\) is total states in the model. The recursion in E15 depends on the fact that the probability of being in state \(j\) at time \(t\) and seeing observation \( o_t \) is equivalent to the sum of forward probabilities for all possible predecessor states i, weighted by the probability of making each transition from that predecessor,, E15 has an initial condition: $$ \alpha_j(1) = P(S_j \,|\, S_1 ) \,\,\times \,\, P(o_1 \,|\, S_j ) \qquad\qquad \text{(E16)} $$ And a final condition: $$ \alpha_N(T) = \sum_{i=1}^N\, \alpha_i(T) \, \times \, P(S_N | S_i ) \qquad\qquad \text{(E17)} $$ Though generated in passing, \(\alpha_N(T)\) is actually our target variable in the evaluation step: it is the final forward probability, which is also the total likelihood of an observation sequence \(O_i^{(A)}\) given a speaker model \(\theta_A\): $$ P(O^{(A)} \,|\, \theta_A ) = \alpha_N(T) \qquad\qquad \text{(E18)} $$Calculating the backward probability
The backward probability \(\beta_j(t) \)is the conditional probability of observing the remainder of the observation sequence from now to the end ( \( O_r = o_{t+1}, ..., o_T \) ), given that the model is in state \(j\) at time \(t\): $$ \beta_j(T) = P(\, O_r \,|\, s(t)=j, \, \theta_A) \qquad\qquad \text{(E19)} $$ Again, in practice an efficient recursion is used to compute $$ \beta_j(T) = \sum_{j=1}^N \,\, P(S_j \,|\, S_i) \,\times\, P(o_{t+1} \,|\, S_j ) \,\times\, \beta_j(t+1) \qquad\qquad \text{(E20)} $$ Where the computation begins at the final time \(\beta_j(T)\) and ends by computing the backward probability of the first frame \(\beta_j(1)\).Calculating the smoothed expectation
Lastly, the product of \( \alpha \) and \( \beta \) yields us a maximum-likelihood of the sequence \(O\) at an occupied state \(j\): $$ \alpha_j(t) \beta_j(t) = P(O, s(t)=j \,|\, \theta_A) \qquad\qquad \text{(E21)} $$
3.2.2. Baum-Welch re-estimation
From the statement of the learning problem, E14, we know that finding optimal parameters for a HMM speaker model involves the , we need the probabilities of state occupation at each time. The algorithm is as follows:
1. For each training sequence:
1.1. Calculate the forward probability, by E16.
1.2. Calculate backward probabilities, by E21.
1.3. Weight the contribution of the current sequence `O` to the
model’s transition function.
1.4. Weight the contribution of the current sequence `O` to the
model’s emission function.
1.5. Calculate new model parameters from the weighted average of
[1.3] and [1.4] (that is, the initial state probabilities,
transition probabilities, and emission probabilities.
We derive 1.3 and 1.4 from the product of the forward and backward probability densities (E22) as follows. The probability of state occupation ( L_j(t) ), for the chance of being in state (j) at time (t), is computed from the product of the forward and backward probabilities (E21) by the following:
\[\begin{align*} L_j(t) &= P(\, [s(t) = j] \,|\, O^{(A)}, \, \theta_A) \\\\ &= \frac{ P(\, s(t) = j \,\,|\, \theta_A) } {P(O \,|\, \theta_A )} \\\\ &= \frac{ 1 } {P(O \,|\, \theta_A )} \, \times \, \alpha_j(t) \beta_j(t) \end{align*} \qquad\qquad \text{(E22)}\](That is, the inverse of the total likelihood multiplied by the forward-backward product, E21.)
We can then set the means for each Gaussian of each state: the estimated mean \(\hat{\mu}_{jg}\) of the \(g\)th Gaussian of state \(j\) is a weighted average of the probability of this vector \(o_t\) given \(L_j(t)\):
\[\hat{\mu}_{jg} = \frac{ \sum^T_{t=1} {L_j(t)} \,\times\, p(o_t) } { \sum^T_{t=1} {L_j(t)} } \qquad\qquad \text{(E23)}\]Given this re-estimated mean, we can find the covariances as the following weighted average:
\[\hat{\Sigma}_{jg} = \frac{ \sum^T_{t=1} {L_j(t)} \,\times\, ( o_t - \hat{\mu}_{jg} )^2 } { \sum^T_{t=1} {L_j(t)} } \qquad\qquad \text{(E24)}\]For long sequences of vectors, repeatedly multiplying probabilities as in E17 and E20 leads to very small probabilities, and thus a risk of underflow: the probabilities are thus logarithms, and E22 (and E26 below) are calculated in log arithmetic.
4. Hidden Markov modelling for linguistics
HMMs were originally used for automatic word recognition (i.e. for modelling dictionary words and outputting the most likely word or sentence given an input vector).41 Since we’re focussed on speaker recognition instead, this bit covers the use of HMMs in speaker verification, only introducing the statistical machinery in common.
For example, in word-recognition applications, the point of multiple HMM states is to ensure that only certain patterns of phonemes or words are accepted (representing the constraints of the morphology of the language, or its grammar). In our case, the states capture, instead, distributions of acoustic evidence over time: roughly, the speaker’s overall typical wave over the course of pronouncing a word.
A primary motivator for using HMMs in linguistics is that the models are doubly stochastic, i.e. they are capable of modelling simultaneously two domains of speech, like time and frequency.
The Markov PFSM is our representation of temporal changes in speech (for instance changes in speech rate or intonation); the emission GMM of each state represents the variation in the spectral properties of a given linguistic token.
In general, you can use HMMs to model linguistic phenomena by building a recogniser for each desired ‘phone’ (isolated linguistic unit). This is shown in Fig.8. A recogniser consists in a trained set of ‘phone models’, a series of unlabelled novel inputs (the test set) and some way of categorising the model’s output according to the most likely unit (the transcriptions). The recogniser is, then, a map function for mapping speech (represented as sequences of vectors) to symbol sequences.
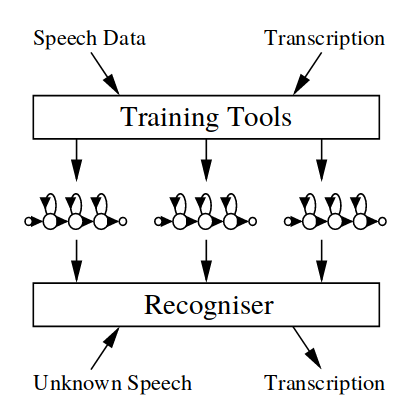
Fig.8 - The general form of a HMM recogniser. Here, 3 HMMs are trained and checked.
Agnostic about the entity being recognised (words, phonemes, speakers). 42
This general recognition task is not easy. The mapping from linguistic symbols to speech waves is many-to-one; i.e. different symbols can easily give rise to similar speech sounds (consider “foxhole” and “Vauxhall”, or “Lady Mondegreen” and “laid him on the green”).
And the statistical noise between two waveform tokens of the same symbolic unit is often very great, due to variations
between speakers, between context (speaker mood, social cues) and paralinguistic effects (pitch,
intonation, speech rate). These problems make parameter optimisation and probabilistic judgment (e.g. offering multiple scored hypotheses) so key to recogniser performance.
Assumptions
We can only use HMMs for linguistic purposes given some key assumptions, including two important approximations to the speech signal:
- Stationarity: In order to have distinct training and testing phases for our models, we assume that a speech signal can be well-approximated as a concatenation of static distributions (more formally, as a ‘piecewise stationary process’, a stochastic process whose joint probability distribution does not change over time). This requires us to first ‘window’ the signal into discrete and periodic units, on the order of 10ms long: we assume stationary of the waveform over this short duration (see section 5.2).
- Markov process: that the sequence of observed speech vectors corresponding to each word is generated by a Markov model (that each state depends only on the most recent antecedent); and, as a corollary, that the information lost by making the Markov assumption for speech does not occlude important patterns in the speech data, at least for many stochastic purposes. (That is, we assume that the full, delicate N-gram chains of real contextualised natural language are not the only property of interest.)
- Representativeness: that the training data that will determine the model parameters is properly representative of the linguistic unit being modelled.
- Unidirectionality. That the only possible transitions are forward in time, since speech is a temporal sequence. (i.e. Left-Right models.)
4.1. HMMs for speaker verification
Using HMMs to authenticate “voice-prints” involves similar machinery to the
speech recognition case, but uses speakers as the ‘words’ to be recognised. The models can quite
reliably distinguish speakers through the use of characteristic differences between the speech of
different people (inter-speaker variability). The general speaker-verification problem is simply:
Given a segment of speech, [\(O\)], and a hypothesized speaker, [\(A\)], the task of speaker detection… is to determine if [\(O\)] was spoken by [\(A\)].43
A system for verifying speakers requires the following subsystems:
- An acoustic analysis subsystem, which extracts many ‘features’ (vector measurements) from each signal at regular intervals (frames).
- A modelling subsystem, which creates a model of speaker \(A\) and estimates optimal parameters using training outputs from subsystem (1).
- A scoring subsystem, which determines how well each test output from (1) fits the model.
- A decision subsystem, which uses the output of (3) and a pre-specified precision threshold to authenticate or reject the speaker \(A\) .
The acoustic analysis step is covered in section 5.2; the modelling is as outlined above in 3.2 (though actually, simple GMMs are the dominant approach for text-independent speaker verification). 44
One simple scoring measure is to evaluate the conditional probability (the likelihood) of an utterance being generated by the model and to compare this . And a simple decision measure is the hypothesis test between \(h_0\) (“the utterance \(O_i\) is not by speaker \(A\)”) and \(h_1\) (“the utterance \(O_i\) is by speaker \(A\)”):
\[v_i^{(A)} = \frac{ P(\, O_i^{(A)} \,|\ \theta_A) } { P(\, O_i^{(A)} \,|\, h_0 ) } \qquad\qquad \text{(E25)}\]The ratio is then compared to a threshold value; if (v_i^{(A)}) exceeds it, ( O_i^{(A)} ) is accepted as an utterance by (A); if it does not, the null hypothesis is not rejected.
This approach – taking the likelihood ratio of an utterance, conditional on speaker models – was adapted for use in detecting accommodation by the SSSV experiment, on which the present work relies.
4.2. HMMs for analysing accommodation
Finally, our particular method. In speaker verification modelling, each HMM is a series of statistical patterns representing the
‘acoustic realisation’ of a modelled speaker (i.e. a series of distributions summarising the speaker’s
characteristic speech vectors). Take the components of our speaker HMMs as representing the
following:
- The hidden process: the non-conscious and contextual factors that determine the change in a speaker’s typical utterance, over time.
- Each state: an artificial division of each word into temporal chunks.
- Emitted observations: a 12D feature vector; one frame of an utterance by \(A\).
- Time unit: one frame taken from one word by A (in our case, 10ms).
- The whole model: one speaker A’s ‘typical’ (word-independent) utterance pattern.
This adapts the (E25) approach for verifying a speaker, with one modification; since we know which speaker uttered each utterance, we can compare the likelihood \(P(\, O_i^{(A)} \,|\ \theta_A)\) generated by the model of the actual speaker of to the likelihood \(P(\, O_i^{(A)} \,|\ \theta_B)\) of their interlocutor’s model generating \(O_i^{(A)}\).
Call this the point estimate of speaker distance \(d_i^{(A)}\) for an utterance by \(A\):
\[d_i^{(A)} = \frac{ P(\, O_i^{(A)} \,|\ \theta_A) } { P(\, O_i^{(A)} \,|\, \theta_B ) } \qquad\qquad \text{(E26)}\]Where values of \(d_i^{(A)} > 1\) represent model \(\theta_A\) explaining \(O_i^{(A)}\) better than \(\theta_B\) does.
The speaker-distance thus serves as a point estimate of the relative distance of \(A\) from \(B\) at the time of utterance \(t_i^{(A)}\). This ratio is calculated for each utterance by \(A\), and the point estimates are then correlated over time by Spearman’s rank correlation coefficient \(\rho\) :
\[\rho \, \large(\,d_i^{(A)}, t_i^{(A)} \, \large) \,=\, 1 - \frac{6 \,\times\, \Sigma(d_i^{(A)})} { N_k (N_k^2 - 1) } \qquad\qquad \text{(E27)}\]At last, then, we’ve derived our final target variable: the time correlation (E27) of the conditional word-likelihood ratios. If is
statistically significant, it is possible to say that A is converging to (for negative ), or diverging from
(for positive ) B’s characteristic speech pattern.
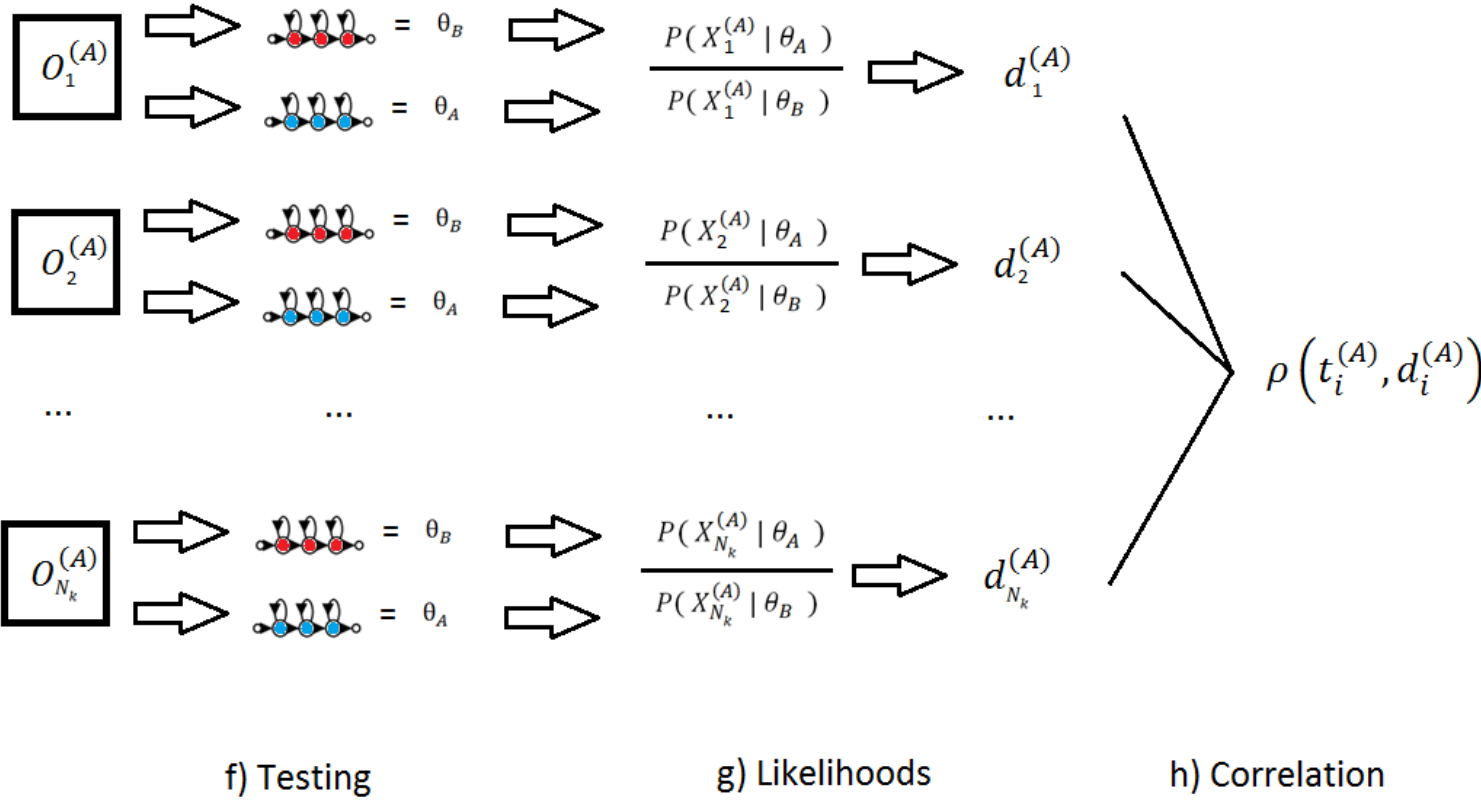
Fig.9 - Illustration of the accommodation analysis conducted for each task k of each speaker A.
Figure 9 illustrates the process of obtaining transcriptions and inferring the presence of
accommodation for each of speaker A’s units of analysis (tasks, k). This is repeated for each of A’s 12 tasks, for each other speaker, and then inferences about the presence and distribution of accommodation are made (see section 7).
5. Present methodology
This section describes the SSSV experiment and elaborates the pipeline used to build and evaluate our HMMs, and thereby infer accommodative effects.
5.1. Experiment design
The experimental work was prior to the present project, but we characterise the setup to clarify the data.
Twelve female volunteers, all native to Glasgow, and previously unacquainted, were assigned into pairs. (These variables were controlled because gender and accent have been shown to have strong effect on accommodation, and because prior acquaintance is a direct confounder of the desired effect. 45 46 )
Conversations were conducted behind screens to minimise the effect of nonverbal cues and visual influences. The data is anonymised with speaker codes (e.g. “ARA14”) which serve to identify the speaker models in the following analyses.
Each pair completed the same twelve tasks from a set of standardised dialogue elicitation tasks, ‘Diapix’, which involve spotting the differences in pairs of pictures of the same scene .47 The order of completion was randomised to prevent any confounding influence from the progression of tasks.
The recordings were manually segmented into 109,730 words by all speakers (9,516 for training and 100,214 for test). Twelve speakers conducted twelve tasks each, so we obtained 144 analysis units. Twelve of these, one task per speaker, were used as training data; thus we end up with 132 ‘speaker-task’ units.
The numbering below refers to the stages defined in Table 1. Stages (a,b) and (c) are the Diapix experiment and the professional manual annotation of the conversations, respectively. The computer segmentation of the conversation files into word files (a trivial operation involving the application of pre-processed annotations) requires no further explanation. The following section elaborates on the implementation of stages (d) through (i).
5.2. Analytical method
For the inference stage, the unit of analysis is the pair-task: that is, accommodative effects are measured for either speaker of a pair, for each of the 12 tasks they completed. But begin by clarifying the way the data is handled on the way to this inference. It involves a hierarchy of four orders:
- i. At time correlation, the unit is the speaker-task: speaker A’s accommodative trend over the course of conducting one Diapix task.
- ii. When evaluating model likelihoods, the unit is the utterance \(O^{(A)}_i\) considered as a single sequence;
- iii. At feature extraction (and for each time step of forward-backward evaluation), the unit is the observation (a vector of coefficients representing one frame within an utterance);
- iv. And the foundational unit is the single coefficient of an observation vector. (This level is not directly manipulated.)
Figure 10 illustrates these four levels by expanding one instance of each unit of analysis into subunits:
(i) Speaker (1) --> Tasks (M)
(ii) Task (1) --> Words (M)
(iii) Word (1) --> Frames (M)
(iv) Frame (1) --> Coefficients (M) </ol>
Fig.10 - Different representations of the same data from one speaker.
That is: Level (i) is the speaker-task level; it shows speaker A’s whole sequence of words, separated by task. Level (ii) denotes the set of words spoken during task 4, Level (iii) shows a word split into its T constituent frames or observations. Level (iv) shows one frame, a vector of D coefficients extracted from that frame of the signal.
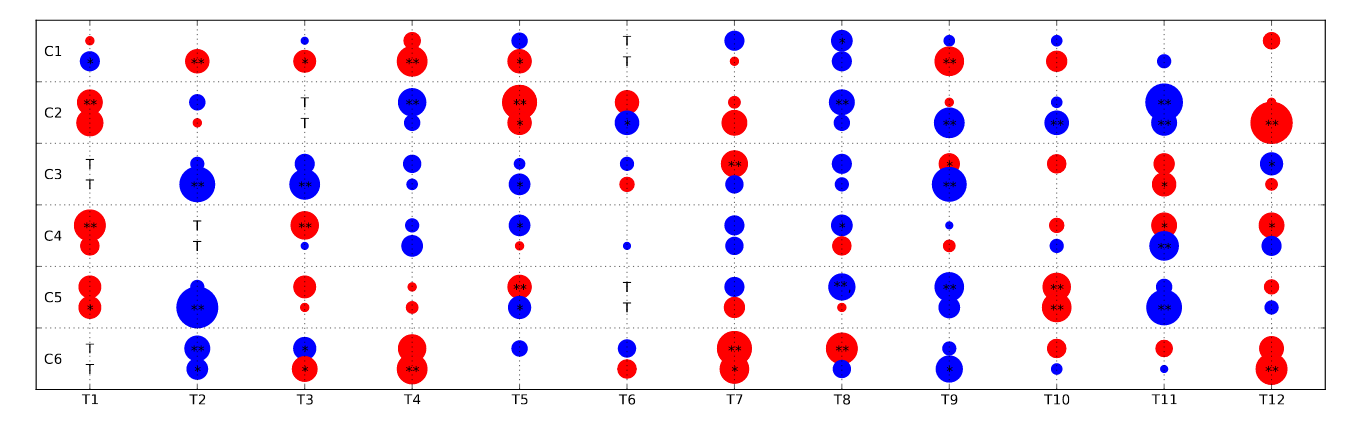
Fig.11 - SSSV experimental results: rows indicate each speaker pair, columns indicate the task.
Blanks indicate tasks used as training data. Bubbles scale to the size of the speaker -task correlation value, with the positive condition in red, negative in blue, and asterisks for significance, * = 5% and ** = 1%.
Finally, for the final analysis, speaker-tasks are paired up according to the original conversational
partners, in order to categorise the disjunctive presence of accommodation for each task, i.e. its
presence in either speaker (see below for the conditioning used). This is Fig.11.
5.2.1. Feature extraction and labelling
Feature extraction is the conversion of the continuous speech waveform into an efficient, expressive lower-dimension representation, for the purposes of increasing the tractability of the data, and perhaps to narrow the analysis to certain spectral aspects of speech. 49
Some definitions:
- Frame: A fixed-length portion of a speech signal, from which to extract a feature.
- Windowing: The subdivision of a signal into successive frames. (Perhaps overlapping frames, as here.) The resulting windows are multiplied by a ‘window function’ that eliminates the signal lying outwith the present interval.
- Extraction rate: how often the processor takes a window from the signal. Here, 10ms.
- Window size: the length of each window. Here, it is 25ms long. So we have overlapping windows.
The vector size must strike a balance between being small enough to permit easy computation (and tuned for relevance, to prevent the capture of spurious variations between tokens of the same linguistic unit which might impede recognition performance); but still large enough to capture salient features of the signal. In our case a sequence of 12-dimensional real-value vectors is output by the models at a rate of one observation per 10ms. The format chosen must also match the distribution assumptions of the models; for example, since our models use Gaussians with diagonal covariance, the features used have to follow the Gaussian distribution and get decorrelated as part of the extraction.
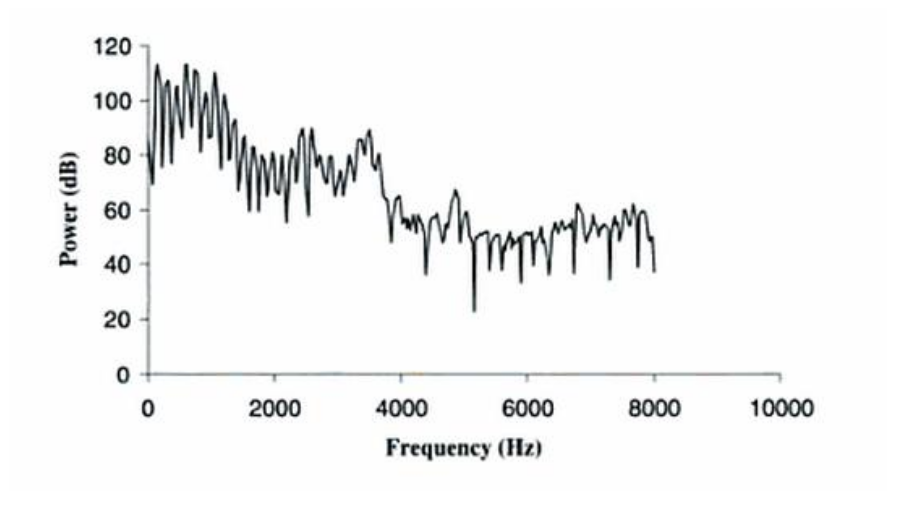
Fig.12 - The power spectral density (or simply ‘spectrum’) of one frame of speech.
The HTK tool ‘HCopy’ performs each feature extraction. This results in a single file ( .mfc, .lpc ) containing all the frames of the source utterance. In our case we also need to store information about the frame number and speaker for each vector; we use separate label files for this purpose, one label per feature file, created with the vector reading tool ‘HList’ (see script 5).
The present work uses two feature extraction techniques to approximate different properties of
speech spectra: Mel-frequency Cepstral Coefficient analysis (MFCC) and Linear Predictive Coding
(LPC).
Mel-Frequency Cepstral Coefficients (MFCCs)
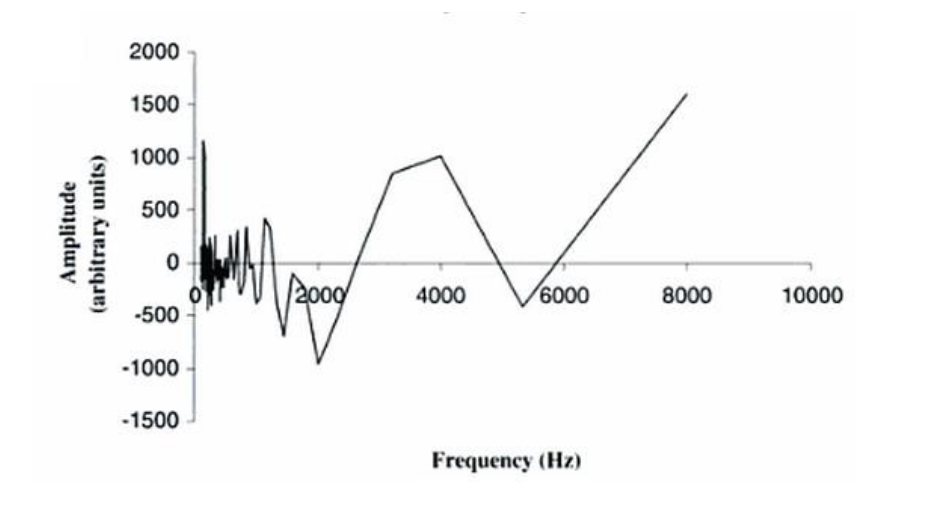
Fig.13 - The cepstrum of the spectrum frame from Fig.12.
MFCCs are a standard feature encoding scheme in speech recognition and speaker-verification. For a Fourier transform of a signal \(F(o_t^{(A,i)})\), its power cepstrum \(C(z)\) is:
\[C(z) = F\, (\,\log \, | \log F(o_t^{(A,i)})|^2\,)^2\]The result vectors themselves are a series of ‘cepstral’ coefficients read off this cepstrum, and are obtained by the following algorithm:
1. For each frame:
1.1. Take the Fourier transform of each overlapping window.
1.2. Summarise this resulting spectrum into fewer energy values,
one for each frequency range required (Mel-scale filter bank).
1.3. Square and take the log of the filterbank energies (F(o_t^{(A,i)}))
1.4. Decorrelate the result using a discrete cosine transform
(i.e. we are plotting the spectrum of the transformed log-spectrum).
This is the cepstrum.
1.5. Read off the required number of amplitudes (D) of the cepstrum,
ignoring the first and counting the next D most significant values.
We thereby trim off less-expressive components of the signal, in passing. This yields a vector of values representing the energy in each frequency band of the current frame.
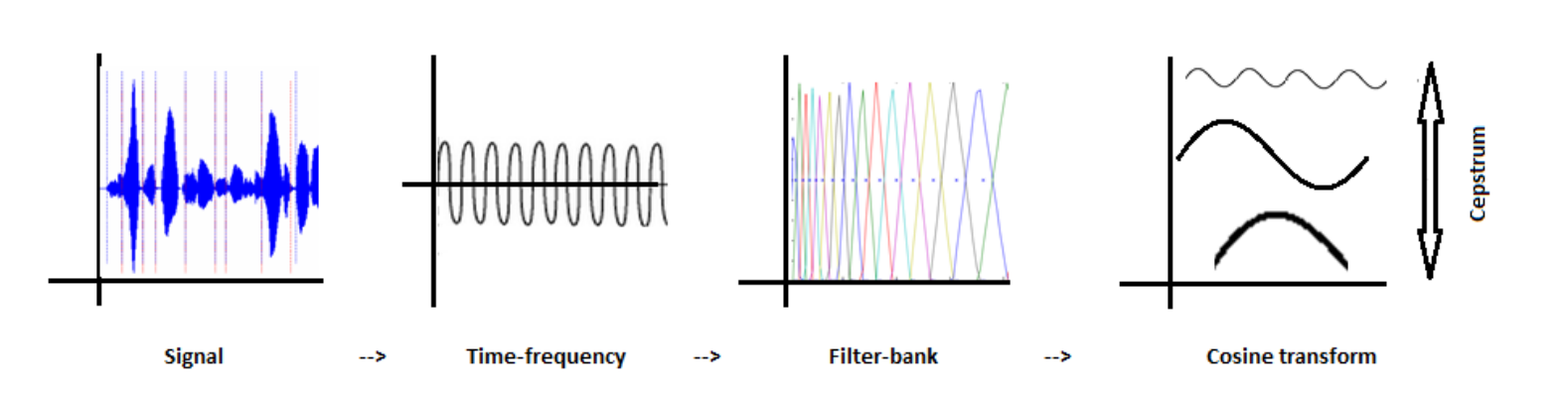
Fig.14 - Plots of the transformations of the MFCC algorithm.
In concrete terms, MFCCs account for
vocal tract properties and phonemes more than for properties that a speaker can control [in order] to imitate, consciously or not, others (e.g., prosody). 53
The mel-frequency scale was developed in order to capture the information processing of the human ear.54 An example of MFCCs being used for holistic measurement of a high-level linguistic phenomenon is Huckvale’s ACCDIST measure for accents.55; using MFCCs as features resulted in accent recognition rates of “up to 92%” for his system.56
Linear predictive coding (LPC)
LPCs are one of the earliest digital speech encoding schemes, known for lossy compression. However, relative to its complexity, linear predictive coding is actually a remarkably effective encoding, and capture by compressing away. Rather than storing the whole chain of a signal’s formant and pitch information, we can numerically model signals by estimating the magnitude of the signal at time \(t\) as a linear combination of the previous \(p\) samples:
where \(p\) is the ‘order’ of the LPC predictor, typically set between 12 and 18. The whole resulting feature vector is thus just a sequence of linear coefficients, plus a set of errors (the “prediction residual”).
The algorithm to extract an LPC vector is incredibly simple: fit a line across each p samples by minimising the size of the prediction residual (for instance by ordinary least squares); then read off the required number of coefficients and residuals.58
To re-synthesise the original speech waveform (or to generate an emission vector during a HMM evaluation) is a simple matter of chaining the stored values of
, which results in an adequate signal, as can be seen approximately in Fig.15:
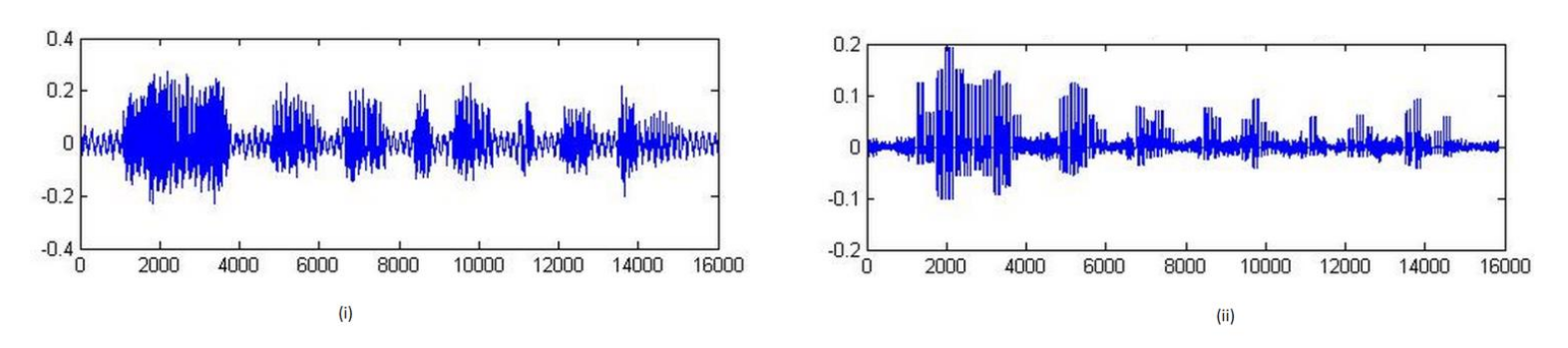
Fig.15 - (i) shows a speech waveform before LPC,
(ii) the waveform after re-synthesis from its LPC vector.59
The p coefficients collectively represent the changing resonances (“formants”) in the vocal tract. The spikes in the prediction residual correspond to the glottal pulses of speech (the part of speech called “voiced speech” including the sibilant and plosive consonants). These occur at a regular rate, (the ‘fundamental frequency’ of speech) and as such can be incorporated to the final LPC by pitch prediction techniques, without losing much of the format’s compression. 60
The advantages of LPCs are the simplicity and efficiency of the extraction process (least squares) and the extremely lightweight storage (far less than 1KB per utterance); this makes them most suitable for speech processing applications involving real-time transmission (e.g. telephone speaker verification) or lookups to large vocabularies. In our case they serve as a useful contrast with MFCCs, capturing dynamic features like pitch and rhythm rather than the shape of the vocal tract.
5.2.2. Model definition and training.
Topology: The first step in modelling an HMM is to define the topology and input type. The optimal
number of states is not known and cannot be readily learned from the data; this then is one of our
design variables.
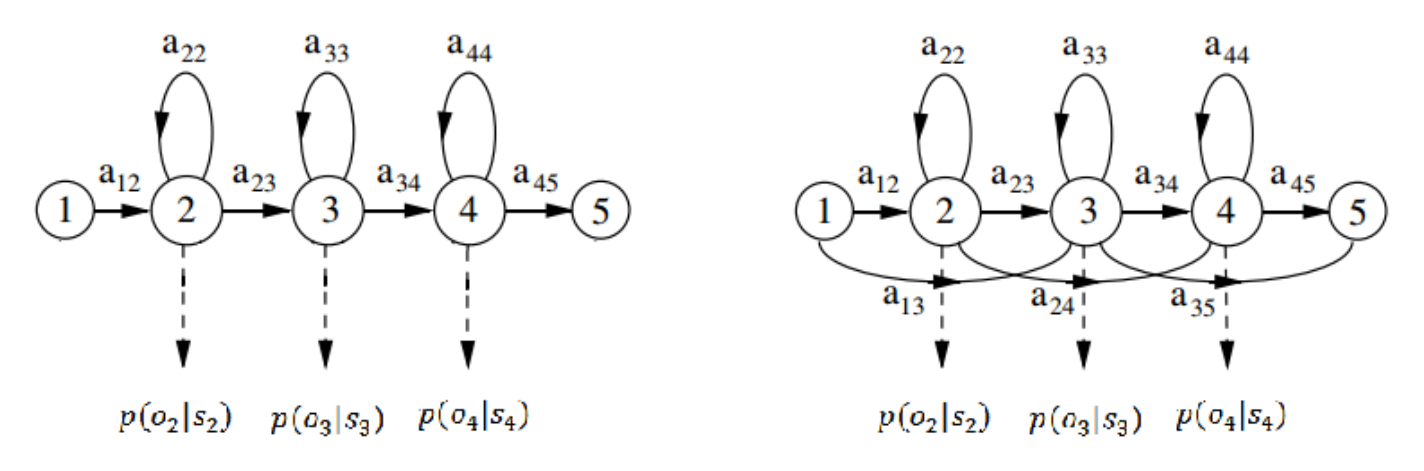
Fig.x - State diagrams illustrating two HMMs N=3, one with, and one without state ‘skips’.
(where \(a_{23}\) denotes the transition probability \(p(s_3 \,|\, s_2)\).)
We take the dimensionality of the input vectors D and set further hyperparameters: the number of Gaussians, \(G = 10\), the alphabet size \(M = 1\). We constrain the transitions to be forward only (by E5) and sequential (by E6).
With these set, we can define a prototype HMM for each speaker; an example of one such prototype definition file can be seen in Fig.4, listing the dimensionality “<VecSize>” and the vector type used for the model, a (presently) arbitary mean and covariance vector for each state, and a transition matrix for the whole model (in which each floating point number at row \(i\) and column \(j\) is ) .
In total we define and evaluate 8 sets of 12 speaker models: one for \(N=1.. 4\) and using MFCC and LPC features.

Fig.16 - The N=2 HMM file from Fig.4, after re-estimation.
(Note that this file requires us to list \(N+2\) states, in order to represent the terminal non-emitting states used by HTK.)
Initialisation: In order to obtain optimal parameters from the Baum-Welch algorithm, we first require good initial estimates for the values of the mean and covariance vectors of each state, in order that the estimates may convergence more precisely to the local optima. We obtain this simply by assigning the global mean and covariance of the training data to the emission distributions and setting the transition probabilities to be equal, a ‘flat-start model’. This is performed with the HTK tool ‘HCompV’ (see script 6).
Training : We perform 10 simultaneous training iterations (‘embedded re-estimation’) with the HTK tool ‘HERest’. This uses the Baum-Welch procedure of section 3.2.2, modified for parallel training as follows:
1. Allocate an accumulator variable for each parameter of each HMM.
2. For each training utterance:
2.1. Construct a composite HMM by joining up the HMMs in sequence.
2.2. For this composite HMM, calculate forward probabilities for all
states j & times t.
2.3. Calculate the backward probabilities for all states j & times t.
2.4. Use 2.2 & 2.3 to compute the probabilities of state occupation
at each frame
2.5. Combining these with the current utterance, by E23.
2.6. Update the accumulators of each parameter by weighting the
existing values by the new utterance, E24 and E25.
3. Use the final value in each accumulator as parameter estimates for each HMM.
Parsing a task grammar into a word lattice
The default mode of HTK is continuous speech recognition; we are instead using the software in a special case of ‘isolated word recognition’ (where no specific task grammar constrains sequences of recognitions, as there is in sentence-level ASR).
Even so, the parameters of the relevant HTK shell ‘HVite’ require a formal syntax (an acceptable sequence of symbols) and a ‘dictionary’ (where the ‘words’ to recognise are defined in terms of models). Our syntax is generated (by ‘HParse’) from the simplest possible Backus-Naur grammar: just one variable in a loop, the speaker code. The dictionary is simply a mapping from the speaker code to the name of the model representing that speaker, where we include one instance of this mapping per state in the HMM. The grammar, though non-functional in our case, is anyway expanded into a graph of possible sequences, a ‘word lattice’ (a set of nodes which represent time steps, and a set of transitions which represent symbol hypotheses).
Fig.18 - Parsing the Backus-Naur grammar into a word network for the HVite recognizer.
5.2.3. Recognition and evaluation
At last we can produce likelihoods for each word of each speaker. 62 The implementation of the forward-backward algorithm (E15) is handled indirectly by the HTK tool ‘HRec’.
Two complete passes are made for each utterance of each speaker ( i.e. two iterations over the set \(O^{(A)}\) ), evaluating each utterance \(O_i^{(A)}\), conditional on both \(\theta_A\) (“self” mode) and \(\theta_B\) (“target” mode). This produces two ‘recognition’ (.rec) files for each utterance, which include its log likelihood and the time it was uttered.
The two log likelihoods are then simply subtracted in order to obtain a point speaker-distance estimate for each utterance.
(In the present method, this is \(log \, P(O^{(A)} \,|\, \theta_A) - log \, P(O^{(A)} \,|\, \theta_B)\) with \(d_i > 1\) indicating superior explanatory power of \(A\) compared with \(B\).)
5.2.4. Correlating the distances
These sets of ratios are paired with the time the utterance began, forming a set of tuples
We use [SciPy] Spearman’s rank correlation coefficient (E27) as a measure of the ordinal trend of these
tuples. \(\rho\) was chosen for robustness to outliers (by comparison to Pearson’s \(r\)).
5.2.5. Inferring accommodation
On obtaining speaker-task values for , we pair the speakers up and assign each of the resulting pair-
tasks one of three ‘conditions’ by the algorithm in Fig.19:
For each pair-task:
1. If both correlations are not significant at 5% :
1.1. Terminate: Null condition for this pair task.
2. If both correlations are significant at 5% and have the same sign, S :
2.1. Terminate: pair are the condition opposite of S.
3. If only one correlation is significant at 5% :
3.1. Call the significant correlation's sign `S`.
3.2. Terminate: pair are the condition indicated by the opposite of `S`.
4. If both are significant at 5% and the signs are mixed :
4.1. Call the correlation with the largest absolute value `C1`.
4.2. Call `S` the sign of `C1`
4.3. Terminate: pair are the condition opposite to `S`.
That is, the ‘positive’ condition is where the largest significant correlation is positive; the ‘negative’ condition is where it is negative; and ‘null’ is where neither correlation is significant. These categories are our final, high-level results for each model set.
We want to detect accommodation at either tail, if either speaker is either converging or diverging reliably over the course of a task. We then attempt to distinguish convergence (the Positive condition) and divergence (the Negative condition) by controlling the detected accommodation for the task’s length (which is a proxy for the pair experiencing difficulty). The hypotheses under test for each pair-task:
\(h_1\) = Accommodation occurs (statistically significant at 5% or 1% level).64
\(h_2\) = Convergence is found more on tasks which take longer.
But are we actually measuring the tendency of speakers to paralinguistically react to each other, or are the models generating spurious patterns? One option to validate a novel computational measure would of course be comparing the results of subjective detecti on for the conversations; however, the small effect size and concomitant expert linguistic attention was beyond this project’s resources. The lack of developed objective holistic measures for accommodation (q.v.) makes it difficult to validate new approaches directly.
We thus investigate and (somewhat) validate the results by two indirect means:
1) the binomial probability of obtaining the n significant results that we did is computed by a cumulative binomial test, giving a sense of the probability or improbability of the models generating the patterns by (pure) chance;
2) looking for significant differences in the average lengths of the tasks in each condition. The latter two offer some validation because of the constant complexity of each Diapix task: if the pair reliably accommodate more when the task is taking longer, this further regularity in the data speaks against mere-chance detection of accommodation.
The analysis is two-tailed: what is measured is the convergence or divergence of paired speaker models over time.
6. Results
The first evaluation was somewhat circular: whether my first analysis (a single-state GMM-HMM with MFCC features) obtained comparable results to the model in Stuart-Smith, Smith et al (2015). (The stochastic process involved in estimating model makes precise replication improbable.)
This is borne out in the replication results below, but should be read as a mere indication of comparability, not bearing on the population.
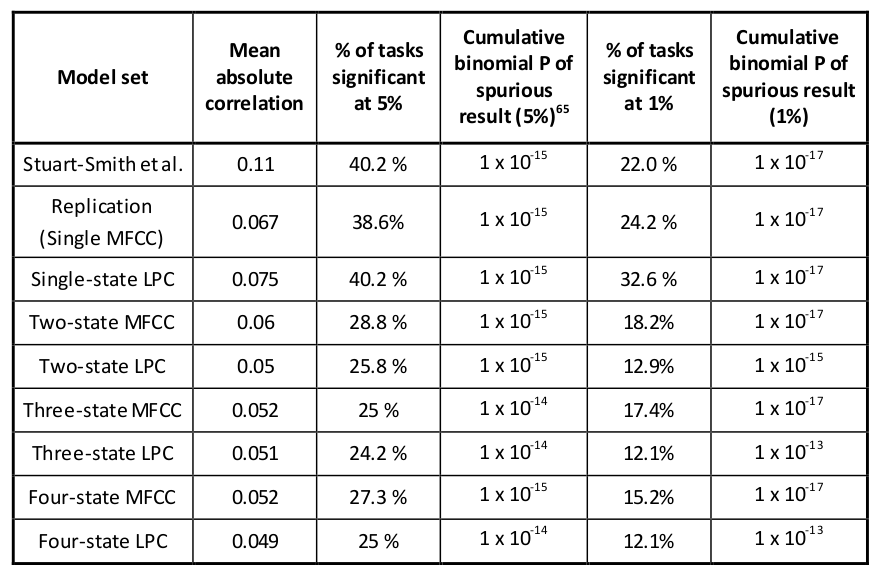
Table 2. Overview of effect size, % correlations and the order of binomial test, for each model type.
We consistently see rates of significant effects with cumulative binomial probabilities less than \(1 \,\times\, 10^{-14}\). Overall, we see a large shift in the rate of significance when we move from the heavily simplified single-state models to multi-state models (as well as when changing the feature type to LPC) and a decreasing mean absolute effect size. The observational nature of the study means we must consider two empirically adequate explanations for this:
- incorporating temporal information adds noise which reliably obscures some accommodative effects which can be captured by single-state models that use the whole sequence of each utterance.
- Or, single-state models generate some spurious accommodative effects; multi-state models generate fewer of these.
The falling effect size may be considered weak evidence for explanation (1). This significant difference between model sets N=1 and N>1 is borne out in the conversation length analysis. The MFCC and LPC analyses obtained a very similar number of significant results at the 5% level (a
mean 39.5 for MFCC and 38 for LPC); the distribution varies, with a weak tendency to reverse the sign of the distance correlation, relative to the other feature type.
Individual Speaker trends
To get a sense of the stability of the results, we can see if characteristic patterns persist for each speaker. Table 3 characterises our speakers across all model sets. Significant effects are seen in all speakers, with some consistency between effects over the model sets:
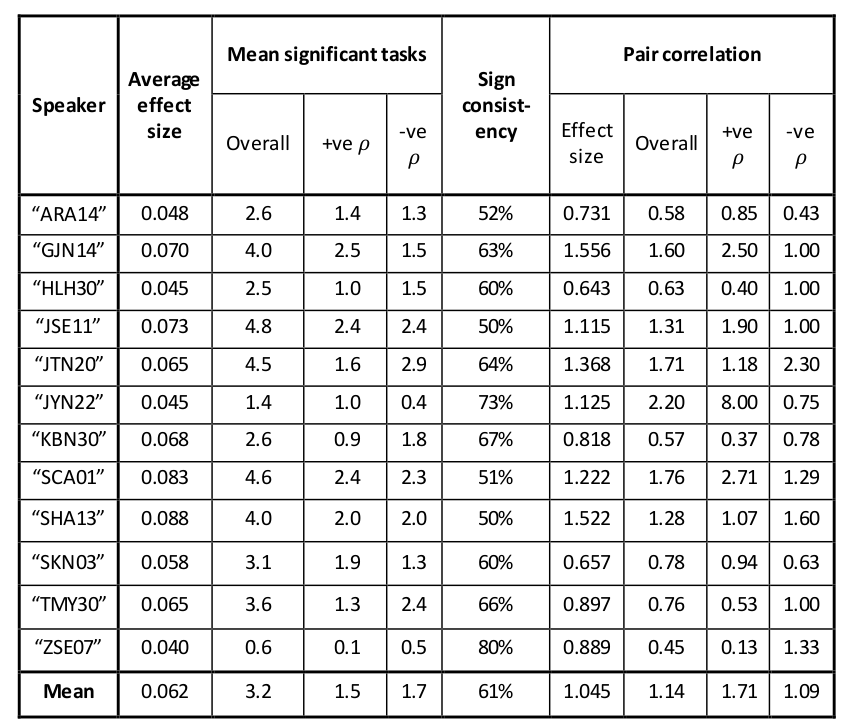
Table 3. Significance and sign of correlations within, and between, speakers.
‘Sign consistency’ is a measure of whether the speaker was a consistent converger or diverger. It is the percentage of all significant speaker-tasks that fall under that speaker’s most common sign (where scores close to 50% thus indicate no strong tendency to either sign) .
The average is 61%; i.e. there is only a mild tendency for a speaker to accommodate in one direction only. The ‘pair correlations’ are an attempt to see if highly accommodative speakers are correlated with higher accommodation in their interlocutor, by effect size, number of significant tasks and sign. It is a simple ratio of the pair’s condition means; thus values near to 1 indicate closeness between the results of a pair. We see a very strong fit between two (absolute) correlation magnitudes, a strong difference between the number of divergent tasks, and a close fit between the mean number of negative results for (which, again corresponds to convergence), but not much closer than the ratio for each speaker’s overall mean.
Conversation length and task difficulty correlations
In Table 4, the ‘Average length’ is simply the average time of each task’s final utterance in seconds, plus or minus the sample mean standard error. The final column is based on the overlap of the average SEM between Positive and Negative conditions. The absence of overlap is taken as a binary cut-off for being able to report a true (average) difference between the Positive and Negative conditions.

Table 4. Average length in each condition, and overlap of SEM for each model type .
Taking non-overlapping standard errors as a criterion for reporting a significant difference between conditions, we can only consider \(h_2\) (the hypothesised effect between length and convergence) confirmed in the single-state MFCC model.
This implies, again, that the link between longer task length and convergent accommodation is obscured by including temporal effects (or, that the link is an artefact arising from considering all the acoustic evidence at once).
7. Conclusion
This study developed HMMs to investigate the presence and nature of linguistic
accommodation. Two hyperparameters were varied, yielding eight permutations and three
interesting results: 1) That multi-state HMMs consistently record fewer significant correlations; 2)
That multi-state models consistently give evidence of the importance of temporal effects in linguistic
accommodation; 3) that the absolute effect size strongly correlates between pairs. In this work, the
interpretation of result (2) is agnostic between two explanations: either that the time part of the
acoustic envelope adds noise that obscures accommodative effects; or else that multi-state models
have higher specificity (rate of true negatives).
The main limitation of the project is its observational nature: in the absence of an external measure,
validation of results is limited to the indirect statistical checks covered in section 5.2.i and section 6.
We had no control group or external measure to identify false positives generated by the models, to
validate any single judgment about a pair-task, or to enable definitive judgment about which of the
above features or models are ‘better’ at detecting the real extent and nature of accommodation.
This inherent limitation to inference aside, the present project’s limitations are mostly a matter of
modelling extensions precluded by haste:
- A larger range of HMMs should have been tried; however, on available computing (and zero budget), 100 hours of training was as far as we could go.
- Pairing speakers created an extra variable, estimated personality, that could have been incorporated: half of the participants were assigned each based on their compatibility as measured by a prior personality survey.66 The above doesn't factor this in.
- The range of models developed fell short of the given dataset’s potential in a few ways: in particular, there was no word-dependence and phoneme modelling. The more ambitious form would have been to create monophone and triphone models of each phoneme, and to reconstruct the accommodation in the phonemes and actual vocabulary spoken by each of the pairs.
- Values for the hyperparameters (the number of Gaussians per mixture and the dimensionality of the vector space) weren't varied. The flat-start initialisation and fixed rounds of re-estimation was also not optimal, relative to allowing dynamic convergence of parameters.
- There was no ‘cross-validation’ (that is, no alternative divisions of the data into the training and test categories, followed by an iteration of training and testing over these alternative categorisations, to more rigorously control for variation within the dataset).
These offer clear hyperparameters for future modelling on similar datasets, including, most relevantly, monophone or triphone modelling (using 40-phoneme HMMs and so being able to break down accommodative effects by changes in each phoneme). This could also guide the development of feature vectors tailored to detect accommodation, by combining acoustic variables the models identified over states.
The statistical technique ‘Granger causality’ – inferring the causal direction of two variables in time-series – could be applied in order to get a better sense of which of the two sides of accommodation (changes in human air-pressure waves and changes in social signals) are the underlying process, if it is fact not fundamentally bi-directional. 67
Bibliography
- Al-Khatib, M. (1995). The impact of interlocutor sex on linguistic accommodation: A case study of Jordan radio phone-in programs, Multilingua, vol.14 (2), pp.133-150.
- Auer and Hinskens (2005), Dialect Change: Convergence and Divergence in European Languages, Cambridge University Press.
- Babel, M. (2009) Selective vowel imitation in spontaneous phonetic accommodation. UC Berkeley Phonology Lab Annual Report 2009, pp.163–194.
- Babel, M. (2010) Dialect divergence and convergence in New Zealand English, Language in Society, vol. 39, no. 4, pp. 437–456.
- Babel, M., Bulatov, D. (2012) The role of fundamental frequency in phonetic accommodation, Language and Speech, vol. 55(2), 231–248.
- Babel, M., McAuliffe, M., and McGuire, G. (2014). Spectral similarity and listener judgments of phonetic accommodation. In Proceedings of the 10th International Seminar on Speech Production.
- Baker, J., Deng, Glass, J., Khudanpur, S., Lee, C.-H., Morgan, N. and O'Shaughnessy, D.
- (2009) Research Developments and Directions in Speech Recognition and Understanding, Part 1, IEEE Signal Processing Magazine, vol. 26, no. 3, pp. 75-80.
- Baker, R. and Hazan, V. (2011) DiapixUK: task materials for the elicitation of multiple spontaneous speech dialogs, Behavior Research Methods, vol. 43(3), pp. 761–770.
- Baghai-Ravary, L., Kochanski, G. and Coleman, J. (2009). Precision of Phoneme Boundaries Derived Using Hidden Markov Models, Interspeech.
- Baum, L. and Petrie, T. (1966). Statistical Inference for Probabilistic Functions of Finite State Markov Chains Annals of Mathematical Statistics, vol. 37, no. 6, pp.1554-1563.
- Bimbot, F., Bonastre, JF, Fredouille, C., Gravier, C., et al (2004) A tutorial on text-independent speaker verification, EURASIP Journal on Applied Signal Processing, vol.2004, pp. 430–451.
- Bishop, C. (2006) Pattern Recognition and Machine Learning, Springer, 2006
- Bousmalis, K., Mehu, M., and Pantic, M. (2013) Towards the automatic detection of spontaneous agreement and disagreement based on nonverbal behaviour: A survey of related cues, databases, and tools, Image and Vision Computing, vol. 31, no. 2, pp. 203–221, 2013.
- Bulatov, D. (2009) The effect of fundamental frequency on phonetic convergence, Phonology Lab Annual Report, University of California at Berkeley.
- Burgoon, JK., Stern, LA. and Dillman, L. (1995) Interpersonal adaptation: Dyadic interaction patterns, Cambridge University Press.
- Camastra, F. and Vinciarelli, A. (2008). Machine Learning for Audio, Image and Video Analysis: Theory and Applications, Springer.
- Cappella, JN., and Panalp, S. (1981). Talk and silence sequences in informal conversations: III. Interspeaker influence. Human Communication Research, vol.7, pp.117–132.
- Casasanto, L. S., Jasmin, K., Casasanto, D. (2010) Virtually accommodating: Speech rate accommodation to a virtual interlocutor, Proceedings of the 32nd Annual Conference of the Cognitive Science Society, pp.127–132.
- Chartrand, T. L., & Bargh, J. A. (1999). The chameleon effect: The perception-behavior link and social interaction. Journal of Personality and Social Psychology, vol.76, pp.893-910.
- Chartrand, TL., Maddux, W., Lakin, J (2005) Beyond the perception–behavior link: The ubiquitous utility and motivational moderators of nonconscious mimicry, in Hassin et al, Unintended thought II: The new unconscious, Oxford University Press, pp. 334–361.
- Chetouani, M. (2014) Role of inter-personal synchrony in extracting social signatures: Some case studies, in Proceedings of the Workshop on Roadmapping the Future of Multimodal Interaction, pp. 9–12.
- Chigansky, P and Ritov, Y. (2011) On the Viterbi process with continuous state space, Bernoulli, vol.17, No.2 (2011), pp.609-627.
- Coleman, JS. (2005) Introducing Speech and Language Processing, Cambridge University Press.
- Davis, KH., Biddulph, R., and Balashek, S. (1952) ‘Automatic Recognition of Spoken Digits’, Journal of the Acoustical Society of America, vol. 24, no. 6, pp.627-642.
- Delaherche, E., Chetouani, M., Mahdhaoui, A., Saint-Georges, C., Viaux, S. and Cohen, D. (2012) Interpersonal synchrony: A survey of evaluation methods across disciplines, IEEE Transactions on Affective Computing, vol. 3, no. 3, pp. 349–365.
- Finlayson, I., Lickley, R., Corley, M. (2012) Convergence of speech rate: Interactive alignment beyond representation, Twenty-Fifth Annual CUNY Conference on Human Sentence Processing, CUNY Graduate School and University Center, New York, USA, pp.24.
- Gales, M., and Young, S. (2007) The Application of Hidden Markov Models in Speech Recognition, Foundations and Trends in Signal Processing, vol. 1, no. 3 (2007), pp.195–304
- Ganchev, T., Fakotakis, N., Kokkinakis, G. (2005) Comparative evaluation of various MFCC implementations on the speaker verification task, Proceedings of SPECOM, vol.1, pp.191–194.
- Giles, H., and Powesland, PF. (1975). Speech style and social evaluation, London: Academic Press.
- Giles, H., Coupland, J., Coupland, N. (1991) Contexts of accommodation: Developments in applied sociolinguistics. Cambridge University Press.
- Huang, X., Baker, J., Reddy, R. (2014), A Historical Perspective of Speech Recognition, Communications of the ACM, vol. 57 No. 1, pp.94-103.
- Huckvale, M. (2007) ACCDIST: An accent similarity metric for accent recognition and diagnosis, in: Müller, C., (ed), Speaker Classification II, Springer Berlin.
- Jayagopi, D., Hung, H., Yeo, C., and Gatica-Perez, D. (2009) Modelling dominance in group conversations using nonverbal activity cues, IEEE Transactions on Audio, Speech, and Language Processing, vol. 17, no. 3, pp. 501–513.
- Kadir, Hamza (2006), Speech compression using Linear Predictive Coding, MATLAB Central FileExchange,
- Lakin, J., Jefferis, V., Cheng, C., and Chartrand, T. (2003) The chameleon effect as social glue: Evidence for the evolutionary significance of nonconscious mimicry, Journal of nonverbal behavior, vol. 27, no. 3, pp. 145–162.
- Lelong A., and Bailly G. (2011). Study of the phenomenon of phonetic convergence thanks to speech dominoes, in Analysis of Verbal and Nonverbal Communication and Enactment, Springer Verlag, pp.280–293.
- Levelt, WJM., and Kelter, S. (1982). Surface form and memory in question answering. Cognitive Psychology, vol.14, pp.78–106.
- Miles, LK, Nind, LK., Macrae, CN (2009), The rhythm of rapport: Interpersonal synchrony and social perception, Journal of Experimental Social Psychology, Volume 45, Issue 3, May 2009, pp.585-589.
- Mistry, D. S., Kulkarni, A. (2013) Overview: Speech recognition technology, mel-frequency cepstral coefficients (MFCC), artificial neural networks (ANN), International Journal of Engineering Research and Technology, vol.2. ESRSA.
- Moscoso, F. (2013), Grammatical Change Begins within the Word: Causal Modeling of the Co-evolution of Icelandic Morphology and Syntax, Department of Linguistics, UC–Santa Barbara, https ://mindmodeling.org/cogsci2014/papers/460/paper460.pdf .
- Munhall, KG., MacDonald, EN., Byrne, SK., and Johnsrude, I. (2009). Talkers alter vowel production in response to real-time formant perturbation even when instructed not to compensate, J. Acoust. Soc. Am. 125, pp.384–390
- Nielsen, K. (2011). Specificity and abstractness of VOT imitation. Journal of Phonetics, vol.39, pp.132-142
- Pardo, JS. (2006) On phonetic convergence during conversational interaction, Journal of the Acoustical Society of America, vol. 119, pp.2382.
- Pardo, J. S., Gibbons, R., Suppes, A., Krauss, R. M. (2011) Phonetic convergence in college roommates, Journal of Phonetics.
- Rabiner, L. (1989) A tutorial on hidden Markov models and selected applications in speech recognition, Proceedings of the IEEE, vol. 77, no. 2, pp. 257–286.
- Rabiner, LR. and Juang, BH. (1991) Hidden Markov Models for Speech Recognition</i>, Technometrics, vol.33, no.3, pp. 251-272
- Reynolds, DA., Quatieri, TF., and Dunn, RB. (2000). Speaker Verification Using Adapted Gaussian Mixture Models, Digital Signal Processing vol.10, pp.19–41.
- Schegloff, E. (1987) Analyzing single episodes of interaction: An exercise in conversation analysis, Social Psychology Quarterly, vol. 50, no. 2, pp. 101–114, 1987.
- Schroeder, MR. and Atal, BS. (1985), "Code-excited linear prediction (CELP): high-quality speech at very low bit rates," in Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), vol.10, pp.937–940.
- Schuller, B., and Batliner, A. (2013) Computational paralinguistics: emotion, affect and personality in speech and language processing, John Wiley & Sons.
- SciPy Community (2014). scipy.stats.spearmanr,
- Shockley K., Sabadini L., and Fowler, CA. (2004). Imitation in shadowing words. Perception and Psychophysics, 66, pp.422–9
- Solanki, V., Stuart-Smith, J., Smith, R., and Vinciarelli, A, (2015) ‘Measuring Mimicry in Task-Oriented Conversations: The More Difficult the Task, the More we Mimick Interlocutors’, conference paper in Proceedings of Interspeech 2015.
- Solanki, V., Stuart-Smith, J., Smith, R., and Vinciarelli, A, (2015b) ‘Utilising Hidden Markov Modelling for the Assessment of Accommodation in Conversational Speech’, conference paper for the 18th International Congress of Phonetic Sciences, 2015.
- Vinciarelli, A., Pantic, M., and Bourlard, H. (2009) Social Signal Processing: Survey of an emerging domain, Image and Vision Computing Journal, vol. 27, no. 12, pp. 1743–1759, 2009.
- Webb, JT. (1969). Subject speech rates as a function of interviewer behaviour. Language & Speech, vol.12, pp.54–67.
- Young, S. J., Evermann, G., Gales, M. J. F., et al. (2006). The HTK Book, version 3.4. Cambridge, UK: Cambridge University Engineering Department.
Comments
Jane Stuart-Smith commented on 07 December 2017 :
Dear Gavin, I am very interested to see this work - could I have it as a pdf or something like that, so I can read it when I am offline? many thanks, Jane
-
~ detail from Bruegel the Elder's
greater "Tower of Babel" - HTK (2006)
- Coleman, JS. (2005) - Introducing Speech and Language Processing, Cambridge University Press, pp.135.
- Their predominance can be seen in the date range between two papers making this claim: Rabiner and Juang (1991), pp.1 - and Gales and Young (2007), pp.197. A formal discussion of HMMs is in section 4 and section 5.
- Stuart-Smith, Smith, Solanki, and Vinciarelli (2015), pp.1. The added parenthesis [] is borne out in their actual analysis.
-
Miles, LK, Nind, LK., Macrae, CN (2009), “The rhythm of rapport: Interpersonal synchrony and social perception”, Journal of Experimental Social Psychology, Volume 45, Issue 3, May 2009, pp.585.
- Chartrand, TL., Maddux, W., Lakin, J (2005) “Beyond the perception–behavior link: The ubiquitous utility and motivational moderators of nonconscious mimicry”, in Hassin et al, Unintended thought II: The new unconscious, Oxford University Press, NY, pp. 334–361
- Babel, M., Bulatov, D. (2012) “The role of fundamental frequency in phonetic accommodation”, Language and Speech, vol.55(2), pp.233.
-
Babel, M., McAuliffe, M., and McGuire, G. (2014). “Spectral similarity and listener judgments of phonetic accommodation”. In Proceedings of the 10th International Seminar on Speech Production.
Babel, M (2009), pp.168 - Bailly, G & Lelong, A (2011) “Study of the phenomenon of phonetic convergence thanks to speech dominoes”, Analysis of Verbal and Nonverbal Communication and Enactment, vol.0, pp.280-293.
- Webb, JT. (1969). “Subject speech rates as a function of interviewer behaviour”. Language & Speech, vol .12, pp.54–67
- Cappella, JN., and Pa nalp, S. (1981). “Talk and silence sequences in informal conversations: III. Interspeaker influence”. Human Communication Research, vol .7, pp.117–132
- Giles, H., and Powesland, PF. (1975). Speech style and social evaluation. London: Academic Press, chapter 2.
- Levelt, WJM., and Kelter, S. (1982). “Surface form and memory in question answering”. Cognitive Psychology, vol .14, pp.78–106
- Smith, Smith, Solanki, and Vinciarelli (2015), pp.4.
- Chartrand, T. L., & Bargh, J. A. (1999). “The chameleon effect: The perception-behavior link and social interaction”. Journal of Personality and Social Psychology, vol .76, pp.896, Study 1
- Auer and Hinskens (2005), Dialect Change: Convergence and Divergence in European Languages, Cambridge University Press, pp.356.
- Jayagopi, D., Hung, H., Yeo, C., and Gatica-Perez, D. (2009) “Modelling dominance in group conversations using nonverbal activity cues,” IEEE Transactions on Audio, Speech, and Language Processing, vol.17, no. 3, pp. 501–513.
- Al-Khatib, M. (1995). “The impact of interlocutor sex on linguistic accommodation: A case study of Jordan radio phone-in programs”, Multilingua, vol.14 (2), p.133-150.
- e.g. the overview given in Lakin, J., Jefferis, V., et al (2003), “The chameleon effect as social glue: Evidence for the evolutionary significance of nonconscious mimicy”, Journal of Nonverbal Behavior 27(3), pp.145-150
- Lelong A., and Bailly G. (2011). “Study of the phenomenon of phonetic convergence thanks to speech dominoes”, in Analysis of Verbal and Nonverbal Communication and Enactment, Springer Verlag, pp.280–293.
- Babel & Bulatov (2009), Bulatov (2012), Pardo et al (2010), Munhall et al (2009), Babel (2010), Shockley et al (2004), Nielsen (2011).
- Gales and Young (2007), pp.2
- This distinction is complicated when we consider that the training of the parameters of generative models is accomplished by discriminative algorithms.
- Coleman, J (2005), pp.112.
- Baum, L. and Petrie, T. (1966) “Statistical Inference for Probabilistic Functions of Finite State Markov Chains” Annals of Mathematical Statistics, vol. 37, no. 6, pp.1554-1563.
- Huang, X., Baker, J., Reddy, R. (2014), “A Historical Perspective of Speech Recognition”, Communications of the ACM, vol.57 No. 1, pp.94-103.
- (see Section 3.1.1 and 5.2 for elaboration and illustrations)
- Rabiner (1981), pp.261.
- HTK Book (2006), pp.9 discusses this special case.
- Note that the forward ‘probability’ is actually a density function.
- Rabiner, L. (1989) “A tutorial on hidden Markov models and selected applications in speech recognition,” Proceedings of the IEEE, vol . 77, no. 2, pp. 259.
- Diagram from Young, Gales et al (2006), p.2. The speech data inputs used are defined in section 4.1.
- Reynolds, DA., Quatieri, TF., and Dunn, RB. (2000). “Speaker Verification Using Adapted Gaussian Mixture Models”, Digital Signal Processing, vol.10, pp.20.
- Reynolds, DA (2000), “Speaker Verification Using Adapted Gaussian Mixture Models”, pp.23.
- Bulatov, D (2009), “The effect of fundamental frequency on phonetic convergence,” University of California at Berkeley, Phonology Lab Annual Report.
- Babel, M (2010) “Dialect divergence and convergence in New Zealand English,” Language in Society, vol.39, no.04, pp.437–456.
- R. Baker and V. Hazan (2011), “DiapixUK: task materials for the elicitation of multiple spontaneous speech dialogs,” Behavior Research Methods, vol . 43, no. 3, pp. 761–770
- Feature extraction is also called front-end processing, quantization, parameterisation, or dimensionality reduction. Or, in the context of speech recognition, signal representation.
- J.S. Bridle and M.D. Brown (1974), "An Experimental Automatic Word-Recognition System", JSRU Report No. 1003, Joint Speech Research Unit, Ruislip, England.
- Stuart-Smith, Smith et al (2015), pp.3.
- Ganchev, T., Fakotakis, N., Kokkinakis, G. (2005). “Comparative evaluation of va rious MFCC implementations on the speaker verification task”, Proceedings of the SPECOM, vol .1 pp.191–194
- Huckvale, M. (2007) “ACCDIST: An a ccent similarity metric for a ccent recognition and diagnosis”, in: Müller, C., (ed), Speaker Classification II, Springer Berlin
- Stuart-Smith, Smith et al (2015), pp.1
- Schroeder and Atal (1985), pp.55
- Diagram from Kadir, Hamza (2006), “Speech compression using Linear Predictive Coding”, MATLAB Central FileExchange.
- Model evaluation, for speech models, is often called ‘recognition’ or ‘transcription’ in the literature.
- The analysis is two-tailed: what i s measured is the convergence or di vergence of paired s peaker models over ti me.
- Smith, Smith, Solanki, Vinciarelli (2015), p.2
- Moscoso, F. (2013), “Grammatical Change Begins within the Word: Causal Modeling of the Co-evolution of Icelandic Morphology and Syntax”, Department of Linguistics, UC–Santa Barbara
Comments
Jane Stuart-Smith commented on 07 December 2017 :
Dear Gavin, I am very interested to see this work - could I have it as a pdf or something like that, so I can read it when I am offline? many thanks, Jane
Tags: stats, social-science